In this article, we will learn Newton’s law of cooling along with the basic statement, definition, explanation, differential equations, formula, and many examples.
Let’s explore!
What is Newton’s Law of Cooling? Definition
Newton’s Law of Cooling Basics
The cooling of numerous objects is often narrated by a theory termed Newton’s Law of Cooling, assigned by the great physicist Sir Isaac Newton.
- Newton made this theory to construct an Industrial thermometer with a large range.
- This Newton’s Law of Cooling in general states that the temperature difference of different bodies decreases significantly with time in respect to their surroundings.
- Since such a pattern is also detected in many laboratory experiments, it has led to an extensive undertaking of this method.
This Newton’s Law is invoked in an extensive range of situations in Applied Science, but the law is also applied in other important areas such as,
- Material Science,
- Atmospheric Physics, and
- high-temperature superconductivity.
So without any further ado, let’s get into a greater aspect of what Newton’s Law of Cooling actually is!
What is Newton’s Law of Cooling?
We all may have observed that when a hot cup of tea is placed in a room in the summer season, the tea inside the cup slowly starts to get cold, but why does it happen in the first place?

Because the temperature of the tea inside is dissimilar to the temperature outside the cup, so there is not much temperature difference.
- Due to this minimal temperature difference, the tea loses its heat (Q), and as it loses its heat, its internal temperature correspondingly reduces, and that’s when it starts to become cold.
- But the same phenomenon is quite the opposite in the winter season where the temperature of the tea is high, but the temperature of the surrounding room is cold, so the tea rapidly gets cold since there is a large temperature difference between the tea and the surrounding temperature.
This rate of loss of heat of a particular body directly proportional to the temperature difference between the body and the surrounding fluid medium is called Newton’s Law of Cooling.
Simplifying the Concept of Newton’s Law of Cooling
To understand Newton’s Law of Cooling, we all should be familiar with the first and the second Laws of thermodynamics.
- The First law of thermodynamics states, the net heat provided by the surrounding on the system is equal to the net work done by the system on its surroundings when the system undergoes a thermodynamic cycle.
- The Second law of thermodynamics can be stated as follows, for a spontaneous process, the overall entropy change of a system plus its surroundings will always increase. In this law, the energy flows in the form of heat or work from one system to another.
Heat transfer is also an important aspect in understanding Newton’s Law of Cooling as it is beneficial in every side of day-to-day life such as technology, hygiene, cooking, transportation, etc.
Heat transfer is a very extensive subject used in many fields of engineering, and the notion of heating and cooling is crucial in the building of every design and machine having moving parts.
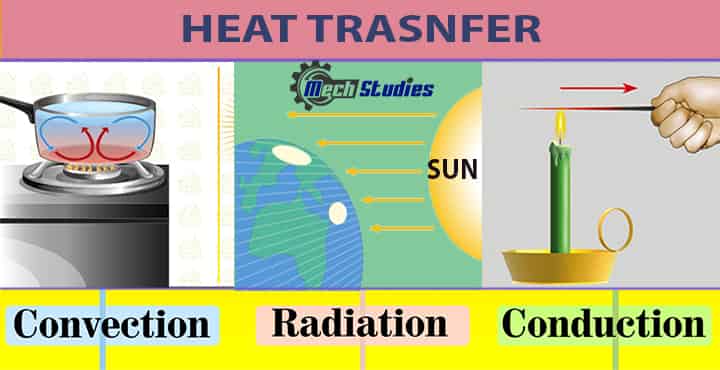
The types of methods through which the heat transfers are conduction, convection, and radiation.
- In solids, the heat is transferred from one point to another through conduction, whereas in liquids and gases it takes place by convection.
- Heat transfer can also take place by radiation where there is not any particle’s involvement in transferring heat.
- That is why in any vacuum or empty space heat transfer occurs through radiation. Newton’s Law of Cooling applies to the second type of heat transfer i.e. Convection.
Let’s see conduction, convection & radiation at a glance,
Conduction
- The process by which heat energy is transferred from one point to another through the direct contact of atoms or molecules.
- It generally occurs in solids and liquids where the particles are generally closer than in the gases where the particles are farther away.
Convection
- It is the process of transfer of thermal energy from one point to another through the movement of atoms and molecules of a liquid or gas.
- Two types of convection are natural convection and forced convection.
Radiation
- It is an energy coming from a particular source and traveling through space with the speed of light.
- The energy has electric and magnetic fields linked with it and also has wave-like properties due to which it can also be called “electromagnetic waves”.
But it was in the early 1740s that Scientists found out that Newton’s law does not apply to all contexts, and it is still much of a debate throughout the 18th and 19th Centuries, particularly with radiation.
Therefore, scientists discovered three well-defined models (laws of Cooling) that aim to relate the cooling of different thermal systems in laboratory environments.
- Newtonian Cooling
- Dulong- Petit Cooling
- Newton- Stefan Cooling
Since all the above models vary on the basis of different bodies, surroundings, and systems, hence in this article we would only be looking into the general Newton’s Law of Cooling.
Newton’s Law of Cooling Differential Equations, Formula Derivation
For the above example of Tea, the following formula can be used according to Newton’s Law of Cooling.
The mathematical equation is,
Rate of cooling ∝ ΔT
This equation can also be written as, dT/dt = – k (T-Ts)
- T : Temperature of the body (of which the rate of cooling has to be found out)
- Ts : Temperature of the surrounding fluid near the body (Most commonly air)
- k : Proportionality constant (In some cases, Heat transfer coefficient)
(Proportionality constant also depends on the specific heat of the object, how much surface area is exposed to the object, etc.)
Notes:
- Here the negative sign is attached to the constant because in this case, as time increases, the heat is decreased, i.e. T ≥ Ts
- The Temperature’s S.I Unit is Kelvin (K), hence temperature is calculated in degrees Celsius often.
Equation 1
dT/dt = – k (T-Ts)
- Since the above equation is a Separable differential equation, with the help of this equation and solving it more, we can get a general solution, i.e. we can get the Temperature Tα or the Rate of Cooling dT/dt as per our requirement.
Now let’s divide both sides by (T-Ts) and multiply by dt
We get,
- dT/(T-Ts) = – k dt
By variable separable and Integrating,
- log (T-Ts) = -kt + log c
Taking log on the other side,
- (T-Ts) = e-kt + log c
- (T-Ts) = e-kt+ elog c [as ea+b = ea. eb]
- (T-Ts) = e-kt c
- (T-Ts) =c e-kt
Equation 2
T = Ts + c e-kt
Where,
- T = Temperature of the body (of which the rate of cooling has to be found out)
- Ts = Temperature of the surrounding fluid near the body (Most commonly air)
- c = Arbitrary constant
- k = Cooling constant (depends on Heat capacity, nature of body or body area)
- t = Time in seconds
This Newton’s law of cooling formula (Equation 2) can give us the temperature of the body when there is a great difference in the temperature between the body and the surrounding.
Now, let’s see Newton’s law of cooling derivation according to Stefan’s law,
According to Stefan’s law, the rate of loss of heat can be calculated as below,
Equation 1
E = ε σ [T4 – To4]
Where,
- ε = Emissivity
- σ = Stefan’s constant
- T = Absolute temperature of the hotter body
- To =Absolute temperature of surrounding medium
(Here the condition is that the T is slightly greater than To )
Let T – To = ΔT
Equation 2
T = To + ΔT
Now comparing equations 1 and 2 we get,
- E = ε σ [T4 – To4]
- E = ε σ [(To + ΔT)4 – To4]
- E = ε σ [To4(1 + ΔT/To)4 – To4]
(1 + ΔT/To)4 ≈ 1 + 4ΔT/To [ Here, the higher order of ΔT/To is neglected]
So, we can write,
- E = ε σ [To4(1 + 4ΔT/To) – To4]
Now after opening the brackets,
- E = ε σ [To4 + 4ΔT. To3 – To4]
- E = ε σ [4 ΔT. To3]
- E = 4 ε σ To3 ΔT
Hence, we can say that 4 ε σ To3 is constant.
So,
- E ∝ ΔT [as 4 ε σ To3 is constant]
- E ∝ (T – To)
So we prove that,
The rate of loss of heat is directly proportional to the temperature difference.
- Thus with the help of Stephan’s law, we can derive Newton’s law of cooling.
Applications of Newton’s Law of Cooling
Important applications of Newton’s Law of Cooling are as follows:
Forensic Science
One of the crucial applications of Newton’s law of cooling can be noticed in forensic science where the detective and the forensic scientists jot down the temperature of the dead body and the surrounding room temperature of the crime scene.
These temperature values are then put in the mathematical formula obtained by Newton’s law of cooling because of which we can determine the actual time of the victim’s death.
Different types of Fluid Cooling
Newton’s law of cooling is applied to calculate the cooling of different types of fluids as it can assist us in predicting how much time it will take for hot fluids or beverages to cool down at a certain temperature.
- It can be seen that when a very hot beverage is kept at room temperature, then within the first few minutes it cools down quickly.
- This happens due to the large temperature difference between the beverage and the surrounding room temperature, hence the rate of cooling is directly proportional to it.
Correspondingly, when the temperature difference is low, the rate of cooling is decreased. Finally, to calculate the time involved in such processes can be calculated through Newton’s Law of Cooling.
Canned food Packaging
The food or the liquid packed in tin cans or plastic jars is always checked with the temperature in the production line. This is to prevent the growth of microorganisms that damage the food or contaminate it.
- Canning is a common methodology for food preservation.
- All this can be achieved with the help of Newton’s Law of cooling in which sterilization is carried out on the food product while cooking and thermal shock is given eliminating 100% of bad bacteria or microorganisms.
- The food packed in airtight sealed containers are always subjected to heat treatment, in this manner we can store the food for a particular number of days without the food getting damaged.
Calculating temperatures of high degree metals
Let’s consider the case of a blacksmith when he heats a piece of metal to a substantially higher temperature, but at the time of noting down the temperature of the heated metal, he notices that there is no such measuring equipment or thermometer to record such high-temperature values.
Thus, with Newton’s law of cooling, we can measure the rate of cooling of the metal thereafter estimating the earliest temperature of the metal.
Ice-cream melting
In an ice cream factory, the ice cream made and stored out of the freezer immediately starts to melt.
However, this rate of melting can be pre-planned with the assistance of Newton’s law of cooling on the condition that the difference between the temperature of ice cream and the surrounding is studied earlier.
This assists the ice cream distributors and vendors to calculate sufficient temperature and accurately organize their storage facilities.
Limitations of Newton’s Law of Cooling
Several limitations are given below,
- The difference in the temperature between the body and the surroundings should be little.
- The loss of heat happening from the body should be caused by radiation only.
- Newton’s Law of Cooling is also highly inaccurate for very higher temperatures.
- The major limitation is that the temperature should always be constant with the surroundings during the cooling of the body.
High Rated Course
Fundamentals of Heat Transfer Part 1
Fundamentals of Heat Transfer Part 2
Advanced Heat Transfer: Heat Exchangers
Advanced Heat Transfer: Thermal Radiation
Conclusion
Based on the above equations, theories and formulas, we can be able to find different temperature aspects of various bodies and their surrounding area with the help of Newton’s law of cooling in our day-to-day life.
Further Study
Refer to our few other articles,
