What is the Moment of Inertia? Definition, Equation, Formula, Units, Mass, Polar MI

What is moment of inertia? A most widely asked question. When a hollow cylinder, solid cylinder, and sphere of the same mass are freely allowed to roll on a slope which one will reach down first and why? Let’s go through some basics first!

What is the Moment of Inertia? Definition

Before understanding moment of inertia, you need to understand the concepts of the moment, inertia, center of gravity, centroid, and bending moment.

Moment of Inertia Basics

We will learn the basics of moment of inertia. At first, let me ask you one simple question, is torque and moment are same? They are the same thing in physics, but they have significantly distinct meanings in mechanics. They both have the same unit – Newton Meter (N.m).

Let’s see the difference between torque and moment!

Torque	Moment
Torque is a force that may cause an item to revolve around an axis.	A force’s moment is a measure of its ability to cause a body to spin around a given point or axis.
It is used where rotation is involved.	It is used where no rotation is involved.
Applications Turbines, dynamo, shafts.	Applications Bending, bridges, structural designs.

Centre of gravity

• The Centre of gravity is the region on the body where all of the body’s weight acts. For all orientations, a body has just one center of gravity.
• It is designated as C.G or simply G.

Centroid

• The centroid is the point at which the complete area of a planar figure is supposed to be concentrated. In this context, a planar figure is a rectangle, triangle, square, quadrilateral, circle, and so on. Centroid is denoted by the symbol G.
• The centroid and the center of gravity are the same points on a body. If an item is balanced at any point along a vertical line flowing through its center of gravity, it will stay at rest.

Moment of Inertia Definition

It is defined as the quantity indicated by a body resisting angular acceleration, which is the sum of the product of each particle’s mass with its square of the distance from the axis of rotation [Moment of inertia I = Σ m_ir_i²]

• It is denoted by I

The moment of inertia ‘I’ of an element having mass ‘m’ positioned at a distance ‘r’ from the center of rotation equals,

I=mr²

In simpler words, it is the amount of torque required for a certain angular acceleration in a rotating axis.

• It means simply the ratio of angular momentum to the angular velocity.
• Moment of inertia can be written as, I = L/ω,

where,

• I = moment of inertia
• L = angular momentum
• ω = angular velocity

Don’t be confused between inertia and moment of inertia. These are not the same!

Difference between Inertia and Moment of Inertia

• Inertia is the natural tendency of the body to continue in a state of rest or even in a motion at a constant speed along a straight line.
• The mass of the body is a quantifiable measure of inertia. The larger the mass, the higher is the inertia of the body.

Inertia	Moment of inertia
Inertia is defined as an object’s property or inclination to resist changes in its state of motion.	The moment of inertia is a measurement of an object’s resistance to change in rotation. It is stated in relation to a certain axis of rotation.
When force is applied to an object it resists, that’s inertia.	When torque is applied it resists to bend, that’s a moment of inertia
There are 3 types, inertia of direction, rest, and motion	There are 3 types of moments – MI of area, MI of mass, and Polar MI.

Equation or Formula for Moment of inertia and Units

Equation or Formula for Moment of inertia

Let’s consider, a very small ball of negligible mass attached to a rod at the end and it is rotated about a fixed axis.

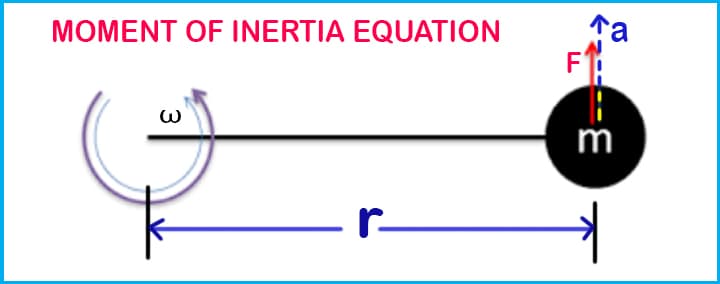
• m = mass (negligible)
• l = length of the rod
• a = acceleration
• F = force acts on the ball

Based on Newton’s Second Law of linear motion,

• Force = mass x acceleration
• F = ma

Now, we can write from the definition of torque,

• Torque = Force x radius
• 𝜏 = F x r = F x r = ma x r =mar [as F = ma]
• 𝜏 = mar

From the angular quantities, we also can write,

• L = I ω
• L = I a/r [as ω = a/r]

We have got two equations,

• 𝜏 = mar
• L = I a/r

By equating these above equations,

• I a/r = mar
• I = mr²

This is the simple equation or formula for the moment of inertia, I=mr²

• Thus, when an object is in angular motion, the mass components in the body are often situated at varying distances from the center of rotation.
• The total MI is the sum of the MI of the body’s mass parts.
• As compared to mass, which is constant for any given body, the moment of inertia is affected by the location of the center of rotation.
• The MI is often determined using integral calculus.
• The moment of inertia (I) is calculated by multiplying the mass of each particle of matter in a particular body by the square of its distance from the axis. When computing angular momentum for a rigid body, the MI is analogous to mass in linear motion. The linear momentum p is equal to the mass m multiplied by the velocity v, but the angular momentum L is equal to the moment of inertia I multiplied by the angular velocity ω.
• The MI is also referred to as the Second Moment of Area.

Let’s assume an object in which two steel balls are welded to a rod and the rod is attached to a bar. If we neglect the mass of rod on which the balls are welded and assume the mass of balls as ‘m’ concentrated at a distance ‘r’ from the center.

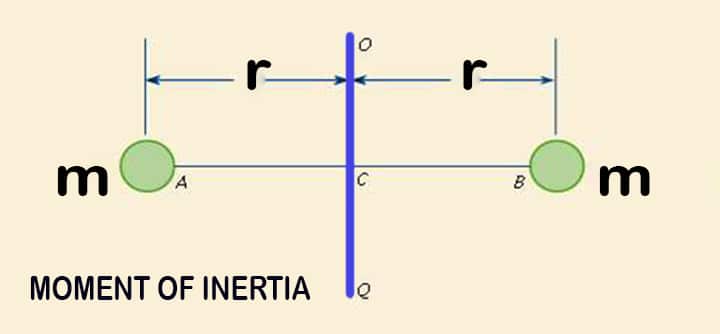
The moment of inertia of the setup will be given by:

I = 2mr²

It is neither scalar nor a vector but it is considered a tensor. ( a generalization of concept vector)

Moment of Inertia Units – S.I Units

Let’s see what is the unit of MI? We have already learned the formula of the equation of MI, I=mr²

Hence, The unit of moment of inertia in the SI unit

• Unit of MI = Unit of mass x (unit of radius)²
• Unit of MI = kg x m² [as unit of mass = kg, unit of radius = m, in S.I unit]
• Unit of MI = kg.m²

Hence, the unit of area MI are kg.m² in SI unit

Moment of Inertia Units – F.P.S. Units

The unit of moment of inertia in the FPS unit

• Unit of MI = Unit of mass x (unit of radius)²
• Unit of MI = lbf x ft² [as unit of mass = lbf, unit of radius = ft, in FPS unit]
• Unit of MI = lbf.ft²

Hence, the unit of area MI are lbf.ft² in FPS unit.

Dimension of Moment of Inertia

The dimension of MI is M.L²

Moment of Inertia Examples

There are so many examples for the moment of inertia, a few of them as illustrated as below,

Practical example – Wheel

• If MI is very large it is very difficult to accelerate in an angular direction.
• If MI is small it is relatively easy to rotate angularly.
• Therefore wheel with less MI accelerates faster. 
• If the mass (m) increases MI increases thus they are directly proportional to each other. So it is much harder to rotate an object with greater mass with the same radius.
• If radius (r) increases MI also increases. So it is much harder to rotate an object with the same mass and greater radius.

Practical example – Rod

• It is easy to spin the rod when it is held at the center.

MI = (ML²)/12

• However, if the cylinder is held at one end, the mass is dispersed quite far from the axis of rotation, making the rotation more difficult.

MI = (ML²)/3

• The moment of inertia of a spinning rod about an axis through an end of a rod is larger than the MI of a spinning rod about an axis through the middle of a rod.
• Thus we can conclude that MI depends on the mass, radius, and axis of an object.
• The mass of a hollow cylinder is distributed farther away from the center. Even if both solid and hollow cylinders have the same mass, the hollow one will be more difficult to accelerate or decelerate. It has a comparatively larger moment of inertia.

Notes for Moment of Inertia

• The MI is a measure of an object’s resistance to changes in rotation.
• It is also described as the ability of a section to withstand bending.
• MI must be specified in relation to a certain axis of rotation.
• It is normally assessed in m⁴ or kgm².

Applications of Moment of Inertia

• Many sections in form of I section or C Section or circular rod or angle section form structural part of any designs. To check the stresses and torque on them we need a moment of inertia.
• Cables mad suspenders in cable suspension or cable-stayed bridges.
• Bracings in multi-story buildings, industrial buildings, overhead tanks.
• Tie member and sag rods in a roof truss.
• Guy wires and collar in steel chimney/stack.
• Mobile towers, electric towers, railway lines.
• Construction of dams.

Mass Moment of Inertia

The mass MI, commonly known as rotational inertia, is a number used to calculate a body’s resistance to a change in rotation direction or angular momentum. It essentially describes the acceleration experienced by an entity or solid when torque is applied. The symbol I_G is commonly used to represent the mass moment of inertia.

• I_G denotes a body’s “mass moment of inertia” about an axis running through its mass center G.
• I_G is defined as: IG= ∫r²dm Units: kg-m² or slug-ft²
• I_G is applied to a variety of rigid body rotation situations, including:

(a) F=ma analysis moment equation (ΣM_G= I_Gα).

(b) Rotational kinetic energy (T = ½I_Gω2)

(c) Angular momentum (H_G= I_Gω)

• I_G is the body’s resistance to angular acceleration. That is, for a given net moment or torque on a body, the larger a body’s I_G, the lower will be its angular acceleration, α.
• I_G also affects a body’s angular momentum, and how a body stores kinetic energy in rotation.
• I_G for a body depends on the body’s mass and the location of the mass. The larger the mass’s distance from the axis of rotation, the bigger the I_G will be. For example, Flywheels feature a hefty outer flange that places as much mass as possible away from the hub.

Practical example – we use ring shape wheels instead of disc shape wheels.

Perpendicular Axis Theorem for Moment of Inertia

This theorem only applies to planar bodies. Bodies that are flat and have very little or no thickness. The theorem states that the moment of inertia of a planar body at an axis perpendicular to its plane is equal to the sum of its moments of inertia along two perpendicular axes coincident with the perpendicular axis and lying in the plane of the body. That means the Moment of Inertia I_z = I_x+I_y

Parallel Axis Theorem for Moment of Inertia

The parallel axis theorem applies to bodies of any form and shape. According to the parallel axis theorem, the moment of inertia of a body about an axis parallel to an axis passing through the center of mass is equal to the sum of the moment of inertia of the body about an axis passing through the center of mass, product of mass, and square of the distance between the two axes. Essentially, the theorem can be mathematically stated as:  I_XX= I_G+Ad²

• A is the cross-sectional area.
• The perpendicular distance between the centroidal and parallel axes is given by d.

Radius of Gyration k_G

What is the Radius of Gyration?

The radius of gyration is occasionally used to express a body’s moment of inertia about an axis. What exactly do you mean by “radius of gyration”? The radius of gyration can be defined as the imaginary distance from the centroid at which the area of cross-section is thought to be focused at the point to achieve the same moment of inertia.

Radius of Gyration Equation & Examples

• It is denoted by k_G
• The following is the equation for moment of inertia in terms of radius of gyration:
  • I = mk²
• The radius of gyration of an area with regard to a certain axis is defined as the square root of the quotient of the moment of inertia divided by the area.
• It is the distance at which the complete area must be considered to be concentrated in order for the product of the area and the square of this distance to match the actual area’s moment of inertia about the specified axis.

To put it in other words, the radius of gyration specifies the distribution of the total cross-sectional area around its centroid axis. The more the area distributed away from the axis, the greater the buckling resistance. A circular pipe is the most effective column section for buckling resistance as its area is scattered as far away from the centroid as feasible.

• Ix = k_x²A
• Iy = k_y²A
• k = I/A

Where is Radius of Gyration used?

The radius of gyration is used to compare the behavior of various structural geometries under compression along an axis. It is applicable in the prediction of buckling in a compression beam or member.

Polar Moment of Inertia

• An entity’s polar moment of inertia is a measure of its capacity to oppose or resist torsion when a specific amount of torque is applied to it along a certain axis.
• Torsion, on the other hand, is the twisting of an entity caused by applied torque. Polar moment of inertia explains the resistance of a cylindrical object (including its segments) to torsional deformation when torque is applied in a plane parallel to the cross-section area or perpendicular to the object’s central axis.
• In situations requiring torsion of cylindrical shafts and slab rotations, the polar moment of inertia is an essential quantity.
• It is a shaft or beam’s resistance to be distorted by torsion as a function of its shape. Rigidity comes from an object’s cross-sectional area not depend on its material.
• The symbol J is  used to signify the polar MI

J = Ix + Iy

To sum it up, the polar moment of inertia is the resistance provided by a beam or shaft when bent by torsion. This resistance is often caused by the cross-sectional area, and it should be highlighted that it is unrelated to the material composition. If the polar moment of inertia is bigger, the torsional resistance of the body will be greater as well. To turn the shaft at an angle, more torque will be needed.

Area Moment of Inertia vs Mass Moment of Inertia

Let’s see the difference between area MI and mass MI, as follows:

Area MI	Mass MI
Area MI is the measure of the capacity of a section to resist bending about the reference axis.	Mass MI is the measure of a capacity of a solid body to resist rotation (i.e angular acceleration) about the reference axis.
More the moment of inertia · Lesser will be the bending stress · Greater will be the beam stiffness · Lesser will be the beam deflection	Lower is the mass MI and hence lesser resistance against its rotation.
It is a property of two-dimensional sections or areas of planes.	It is a property of three-dimensional solid bodies.
Applications Design of beams and structures	Applications Design of gears, gear trains, and gearboxes. (rotating members) Also used in gyroscopic couple and its effect on automobile, ship, airplane.

Conclusion

The moment of inertia is a computation of the amount of force necessary to spin an object. The value can be changed to enhance or decrease inertia. Athletes in sports like ice skating, diving, and gymnastics are continuously modifying their body structure. The MI increases as the radius from the axis of rotation rise, slowing the rotation. If an athlete wishes to improve the speed of rotation, they must lower the radius by moving the segments of the body closer to the axis of rotation, hence lowering the radius and MI. Moment of inertia is used in mechanics, physics, and also in real-life situations to achieve the desired rotational speed.