We have already learned the basics of reciprocating pump and here we will calculate the reciprocating pump discharge, work done, power requirement and slip factors along with sample calculations. I hope you will enjoy this whole calculation parts.
Reciprocating Pump Discharge
Let’s calculate the discharge from the reciprocating pump. Discharge means the fluid flow rate from the pump per second. Now, we already know that due to the revolution of the crank, the piston moves forward and backward which helps to discharge the fluid from the pump. So, the pump will deliver some fluid in one revolution.
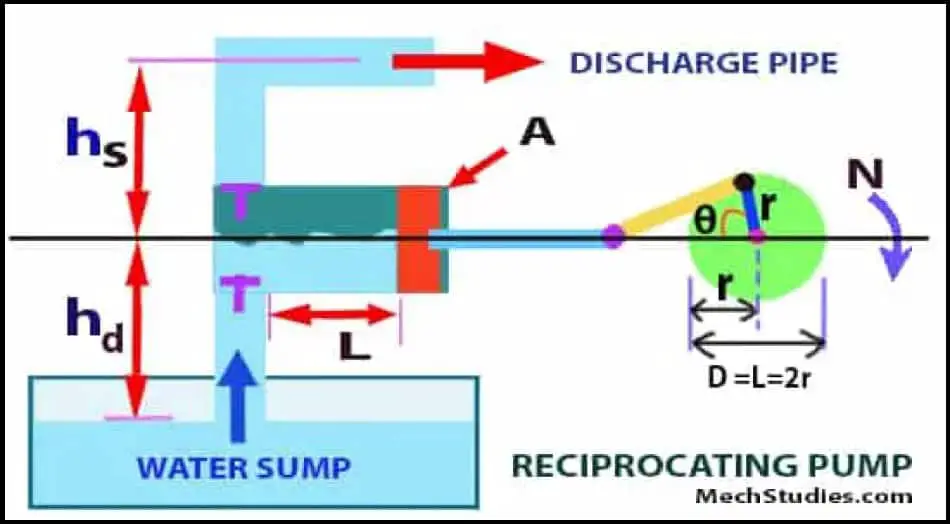
Now, this is not the discharge! Discharge means fluid flow rate per second. So, we have to know that how many revolutions happen in one second and the same can be multiplied with the flow rate per revolution to get discharge per second. Let’s consider,
- A = cross-section area of the cylinder
- r = radius of crank
- L = Stroke length, which means travel of piston in each forward or backward stroke, it equals to 2r, i.e L = 2r [as half cycle rotation or 180 deg rotation gives one stroke]
- V = volume of discharge in one revolution = area x length = A x L, m3
- N = RPM, that means rotation per minute or
- N/60 = rotation per second
- Qh = Fluid flow rate per second, m3/s
Qh = discharge in single revolution x nos. of revolution per second
- Qh = V x N/60
- Qh = A x L x N/60
- Qh = ALN/60
∴ Qh = ALN / 60
This is for single-acting reciprocating pumps, if we derive the equation for double-acting reciprocating pumps, it will be as follows for both sides: Qh’ = Qh1 + Qh2, Where,
- Qh’ = Total discharge of considering both side of piston.
- Qh1= Discharge for Bottom side of piston
- Qh2= Discharge for piston rod area
Now, from single-acting reciprocating pump, we get the value, Qh1 = Qh = ALN / 60
However, the area of the piston rod side area will be slightly less considering the area of the piston rod. Let’s consider, Ap is the area of the piston rod. Hence, the actual area of the cylinder, A’ = A-Ap. So,
- Qh2 = A’LN/60
- Qh2 = (A-Ap)LN/60
- Qh2 = ALN/60 [As Ap is negligible]
Total discharge of considering both sides of the piston.
- Qh’ = Qh1 + Qh2
- Qh’ = ALN/60 + ALN/60
- Qh’ = 2ALN/60
Reciprocating Pump Work Done
Work done means here, the work to be done to lift the fluid per second by the pump. Simply, we can say, work done means the force required to displace the fluid. Work done,
- W.D = Force x Displacement.
- W.D = W x h
Where,
- W.D = Work Done
- W = force = force required to lift or displace the fluid = weight per second
- h = displacement or the height of lifting fluid = hs + hd
- hs = suction head, m
- hd = discharge head, m
- ρ = density of liquid
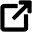, kg/m3 - g = acceleration of gravity, N-m/s2
- Q = discharge of liquid, m3/s
So, to derive the work done for the reciprocating pump, first, we have to derive weight per second. So, Weight,
- W = mg/second
- W = V ρ g/second [Mass = volume x density, or m =V ρ,]
Work Done,
- W.D = W x h
- W.D = V ρ g/second x h
- W.D = (V/second) ρ g h
- W.D = Q ρ g h
- W.D = ρgQh
- W.D = ρg ALN/60 (hs+hd) Joule/Second or watt
This is the work done per second in (S.I unit)
Reciprocating Pump Power Requirement
We have already derived the work done per second, however, we know that power means work done per second. Hence, in this derivation, the power requirement is the same as work done as it states work done per second. Then, the power requirement will be,
- P = Power Requirement,
- P = Work done/Second
- P = ρgQh
- P = ρgQ (hs+hd)
- P = ρgQ (hs+hd)
- P = ρg ALN/60 (hs+hd) watt
- P = ρg ALN/60 (hs+hd)/1000 kW [As 1 kW = 1000 watt]
Slip of Reciprocating Pump
Slip means the loss of capacity due to friction, it can be calculated as
Slip = Theoretical discharge – Actual discharge
- Slip = Qth – Qact
- % of slip = (Qth – Qact)/Qth x 100%
Where,
- Qth = theoritical discharge
- Qact = actual discharge
What is Negative Slip? What is the reason for negative slip?
We know that slip is always positive. But it may be negative as well. Let’s try to understand. If a pump has a suction pipe that is very long, and the delivery head requirement is small. In case, the pump operates at a very high speed, what will happen? There may be a chance of increasing fluid inertia pressure (due to long travel) which causes the delivery valve to open without even completing the suction stroke. This results in fluid at the outlet without completing delivery stroke.
In this case, the actual discharge becomes higher than the theoretical discharge and the Cd value becomes more than 1. Hence, the slip becomes negative. Let us try to see one example, for calculating pump work done, power requirement & slip percentage. Have you thought about the water inside the cylinder? What happens exactly during the suction and discharge strokes? There will be acceleration due to these movements and that can be calculated.
Reciprocating Pump Calculation Examples
Reciprocating Pump Sample Problem
A single-acting reciprocating pump with 200mm piston diameter, stroke length 400 mm, rotational speed 60 RPM. Now, the water is to be pumped at 20 m height. Find out, theoretical discharge. If the actual discharge is 20.2 liters/sec, then what will be volumetric efficiency, slip & power requirement. Mechanical efficiency 80%.
Solution
Answer with explanation,
Theoretical Discharge: Input data,
- d = piston diameter = 200mm = 0.2m
- N = rotational speed = 60 RPM
- L = Stroke length = 400mm = 0.4m
A = cross sectional area = 3.14 x d2/4 = 3.14 x 0.2 x 0.2 / 4 = 0.0314 m2
Discharge of liquid, Qth
- Qth = ALN/60
- Qth = 0.0314 x 0.4 x 60/60 m3/s
- Qth = 0.013 m3/s
- Qth = 13 litre/s
Hence, theoretical discharge is 13lit/s
Volumetric efficiency
- N = volumetric efficiency
- Qact = 11.96 litre/sec
Here,
- N = actual discharge / theoretical discharge
- N = 11.96 / 13 x 100%
- N = 92%
Hence, volumetric efficiency is 92%
Slip
- Slip = (Qth – Qact)/Qth x 100%
- Slip = (13 – 11.96) / 13 x 100%
- Slip = 80%
Power Input: We know,
- ρ = density of water =1000 kg/m3
- g = gravitational acceleration = 9.81 N-s/m2
- Q = 0.013 m3/sec
- H = total head = 20 m
Power required ideal, P
- P = ρgQ (hs+hd)
- P = ρqQH
- P = 1000 x 9.81 x 0.013 x 20
- P = 2550.6 watt
- P = 2.55 kW
Mechanical efficiency, n = 80%
Power input required at actual, P’,
- P’ = Power required ideal / efficiency = P/n
- P’ = 2.55/0.8
- P’ = 3.19kW
Therefore, in this way, the water is sucked and discharged from the sump to the desired location and we can calculate discharge, slip, power inputs, etc. This is a simple calculation to understand the subject matter, you can check reciprocating pump detail calculation as well.
Conclusion
I hope the calculation for reciprocating pump is clear, we request you to read this article after know the basics, which we have explained in our earlier article.
