Solar Water Heater System – Parts, Working, Types, Selection, Benefits

In this article, we will learn about the solar water heater system along with its definition, parts, working, selection, benefits, etc. Let’s explore!

What is Solar Water Heater System? Definition

Solar Water Heater Basics

Environmental sustainability is among the most desired change that humankind should opt for. It includes different efforts that can help to minimize the destruction we are causing continuously.

• It is also quite important as we have to safe keep our environment for our future generation.
• However we are on the path of destruction, but there is numerous successful worldwide effort that helps in protecting the environment.
• Whether it is protecting the ozone layer or keeping a check on the melting of icebergs, scientists and engineers are committing themselves to reverse and minimize the causes of global warming.

Need for the shift towards sustainable energy resources

Environmental sustainability can only be achieved when we will cater to global warming quite successfully. The leading cause of global warming is the carbon dioxide released when burning fossil fuels such as natural gas, oil, and coal.

• It also generates when we burn some of the gases such as nitrous oxide, methane, ozone, HCFCs, CFCs, etc., it is mandatory to think twice while doing these as it makes our environment polluted and causes adverse effects on our health.
• The other reason that is quite prominent for this is the rising population.
• The rapid growth in world population has substantially increased the energy consumption and pollution level in most countries.
• As we know, fossil fuels and oil remain the primary energy source and cannot be kept aside totally.
• We have some energy sources in our atmosphere that can help us cater to pollution and thus global warming.
• Solar energy is among the most prominent ones that can help us attain massive energy and reduce global warming.

This excerpt is all about a sustainable machine that makes our lives easier with no harmful gases. Water heaters are the most common equipment that is used in almost every household. Here we are discussing those water heaters that are operational with the help of Solar Energy.

Solar water heaters are the next generation effective equipment that can help us in catering to our needs as well as causing negligible pollution. This excerpt will provide pertinent information regarding the solar water heater with its working and different kinds of applications.

What is a Solar Water Heater?

Solar Water Heaters is simply a machine equipped with some components such as collectors, tanks, and backup heaters, which cumulatively attract the sun’s radiation and the sun’s thermal energy and convert it into heat energy with the help of a collector panel. The hot water remains at a specific temperature with the continuous supply and heating of cold water.

Parts of Solar Water Heater

Solar water heaters can capture the thermal energy from the sun and use it to heat water for home or industrial applications. There are some of the significant components that are pretty efficient for any SWHs. Are you thinking about buying Solar Products?

Collectors

The collectors are panels responsible for generating heat rather than producing electricity as a photovoltaic cell produces. In this, the sunshine passes through the collector glass and strikes an absorber plate which is a vital component for a Solar water heater.

• Solar hot water systems absorb thermal energy from the sun and use it to heat water for home usage.
• These systems are made of some major components such as collectors, a heat exchanger, a storage tank, a controller system, and a backup heater.
• It has a coating that enables to capture of solar energy, thus converting it to heat.
• This heat generated is then transferred to the fluid that is specifically known as transfer fluid through pipes.

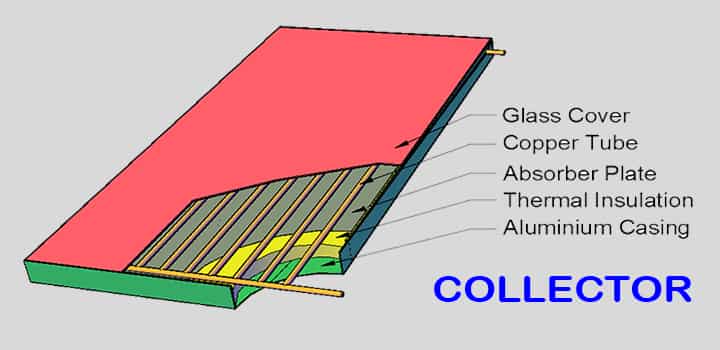
The collectors come in vivid sizes though the number of collectors depends upon the quantity of sunlight the roof is capable of and also on the water consumption of the household or industry. These are manufactures in two styles evacuated and flat plate. Evacuated tube collectors are heavier and fragile but acquire less space, while flat plate collectors are cost-effective but are less efficient.

Controller System

The controller system is specifically used to ensure the water in the tank does not get overheated. It can also help in restricting the cold water from being cycles. This is among the core component that helps in the transfer of fluid by warming them effectively.

Heat Exchanger and Storage Tank

This component helps move the heated water into a series of pipes, ultimately to the tank. It is located inside the storage tank of hot water.

• These are responsible for keeping the water hot, and when the pipes are filled with the same, it passes to the storage tank.
• With this, the hot water is ready to be used for different purposes.

Backup Heater

This is one of the components that provide contingency as it is among the backup systems almost all the SWH are equipped with.

• When there is a sudden weather change, the backup heater comes into play and provides water for the different needs.
• Backup heaters are quite efficient and helpful in the core working of SWH.

How Does Solar Water Heater System Work?

The working of solar water heaters is quite simple. We are simplifying the same by briefly providing the same:

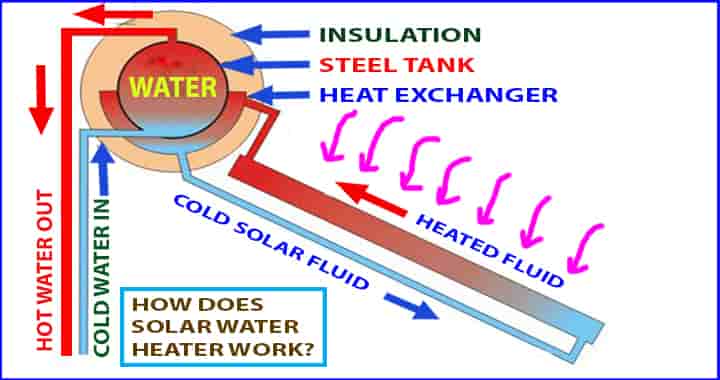
• This Solar water heater system generally can be installed on the roof, and for industrial, it can be both roof or open ground. The collector is attached that faces towards the sun and can be connected to a regular water supply.
• In the pipes connected to the collector, the water flows continuously, and the collector absorbs the solar heat, and as the temperature increases gradually, it gets hot.
• Subsequently, the heated water is stored in the tank for the different usages. In the tank, the water remains stocked up and heated. The storage tank remains insulated, and there is minimal loss of heat.

In the domestic solar water heater, there can be one or more collectors. It can be flat plate or evacuated type collectors. These collectors are equipped with a glaze that attracts solar radiation effectively. The circulation of water continues through the tank, then to collectors, and back towards the tank. This happens due to the density differential between cold and hot water.

Types of Solar Water Heater

There are different kinds of solar water heaters based on structure. They are as follows:

• Copper coil SWH
• Pressurized SWH
• Non-pressure SWH
• Flat plate SWH

Copper Coil Solar Water Heater

Copper coil SWH is one of the sustainable approaches among all kinds of SWH. It depends on the natural circulation of water between the heat exchanger or solar water tank and solar collector.

• In this kind of installation of SWH, the tank should lie above the collector.
• In this, when the water accumulates in the vacuum tube, it gets heated up and becomes lighter.
• It rises effectively to the tank. Gradually the colling water in the tank situates at the bottom of the vacuum tube, which ultimately circulates throughout the system.

Pressurized Solar Water Heater

The pressurized SWH has a structural setup in which the heater combines the collector with the tank. It is also known as an integrated pressurization system in which pressure plays an important role.

• The design of the Pressurized SWH is somehow direct. In this, the water is supplied automatically due to the pressure.
• In this, the water pipe is effectively attached to the system.
• In the solar energy is transferred and absorbed with the help of copper pipe available in the tube.
• Gradually the water gets heated. It is quite essential to install this compact SWH as is among the most efficient type.

Non-Pressure Solar Water Heater

Non-pressure SWH is the best option for household water heaters. These are comparatively less expensive than the pressurized SWH. 

• Non-pressure SWHs use the force of gravity to provide the hot water in the household.
• However, the water is pumped up t the tank with the help of a pump.
• This system is effectively compatible with shower pumps and other household pumps, which are specifically helpful for increasing indoor water pressure.
• The non-pressure SWH is effective for those who require a cost-effective approach for getting hot water.

Flat Plate Solar Water Heater

The flat plate SWH has different components that are quite essential. It is equipped with a metal box which has a plastic or glass cover on the top position. It is also equipped with a dark absorption plate.

• This is among the lightweight flat plate panels that allow par heat transfer.
• These are manufactured of aluminum so that they can withstand dynamic environmental conditions and also the heavyweight load.
• This is among one of the sustainable as well as efficient SWH available in the market.

Proper Selection of a Suitable Solar Water Heater

The selection of a suitable Solar Water Heater is vital as it provides maximum efficiency and increases the machine’s lifespan. This depends on different parameters which should be emphasized effectively. The following parameters can help us understand the prerequisites for selecting a good solar water heater.

• For any household where there is a need for 100liter of hot water per day, then the capacity of the system should be ample.
• If there are multiple bathrooms or a specific usage area, the capacity should be considered per the requirements. The user can decide the requirement of hot water.
• The costing also remains one of the most important considerations. The costing does not only rely on the capacity. The rationality for the higher capacity system should be considered first.
• Apart from that, the cost of a hot water pipeline is substantially high as it comes with proper insulation. The additional cost should also be considered effectively. It can increase the cost to 10-15% of the overall cost.
• The mounting of the collector and the tank should be considered adequate as it defines most of the working efficiency of the SWH. The overall efficiency took a toll on the operational efficiency. If the mounting is not as per the requirements, then it may cause additional maintenance costs.
• The SWH, which are equipped with flat plate collectors, are generally of metallic type. These are specially for longer life than the other types of collectors used. The other types of collectors are not that strong and redundant as they are made up of glass.
• The evacuated type collectors solar water heater systems are comparatively cheaper than the flat plate collectors. The core benefit of ETC-based systems is the proper functionality in the colder regions. It can be very efficient; however, the cost is quite high for this system.  
• Where there are different properties of the water, such as the hardness or chlorine level, then the there should be FPC  based system should be installed as it will help reduce the scaling which occurs due to deposition of dirt. This deposition occurs in the copper tubes of the collectors, which has a backdrop that blocks the flow of water and subsequently reduces the thermal performance of the SWH.

Installation & Maintenance of Solar Water Heater

While installing and maintaining the SWH, some effective points should be given proper care. The following are those points:

• The installation of a solar water heater without any problem depends on different factors such as solar resources, weather, local buildings, and many important safety issues.
• It is recommended to get these things done by qualified personnel or solar types of equipment providers.
• It is quite essential to take proper care of the installed solar-powered equipment as these systems are quite delicate. The passive system does not require much maintenance, while the active system should be given proper care. With the process of glazing, we can achieve optimal maintenance towards the SWH.
• Regular maintenance is the key to increase the lifespan of this SWH. However, these systems should be maintained preferably every 3-5years. These systems need part replacement after ten years or so. It is pretty vital to get a general idea before changing any of the components.

How to Attain the Maximum Efficiency from Solar Water Heater?

Attaining the maximum efficiency for any SWH is quite essential. Not only for the SWH, but any machine should also provide maximum efficiency, making it quite suitable and popular among the users.

• To attain maximum efficiency, it is pretty essential to fulfill some of the operational and mechanical requirements for SWH.
• These requirements not only help to provide maximum efficiency but also helps in elongating the life span for the SWH.
• The following are the operational and mechanical requirements that are pretty important:

The prominent use of solar water heaters is in household applications that do not need specific operational skills. Following those, there are also some of the mechanical requirements that should be fulfilled. Here we mention both of them and some points that help maintain the efficiency of the SWH; these observations should be made to attain peak level.

• It is recommended to consume a maximum of the heated water at once, whether this should be done in the morning or evening. We should restrain ourselves infrequently on or off of the hot water tap. This will lead us to maximum electricity savings, which is one of the sustainable approaches.
• Setting the thermostat at the lowest acceptable temperature is quite important though it depends on the electrical backup.
• There are regions where the household SWH does not get adequately used due to changing weather conditions. In that case, the hot water should be drained, and the collector should be covered effectively. This should be done when the system is totally out of use.
• The collector’s cover should also be covered in the season where there is less consumption.
• Cleaning of the collector is essential as the dust deposition can reduce its overall efficiency. It should be cleaned once a week.
• Domestic SWH does not require critical maintenance requirements. These domestic SWHs can be effectively repaired for occasional leakages and can easily be catered. Apart from that, the industrial SWH needs proper and timely maintenance that should be finalized and rigorously followed.
• Descaling dust accumulated is a core process that should be considered while maintaining the SWH. The use of acid can help to attain the descaling.
• In this SWH, the broken glass of the panel should be replaced to reduce the overall efficiency of the SWH.
• Corrosion is one of the issues that can deplete the lifespan of the SWH. If it is painted and coated, then it should be redone after every specified interval of time.

Benefits of Solar Water Heater

SWHs are prominently used at homes for producing hot water that can easily be used for different household chores. These chores include cleaning, bathing, and washing. These solar water heaters come in different ranges and with different volumes. The standard volume for the same 100-300 liters is suited for domestic application; however, SWHs are also used for different industrial applications. We can quickly get hot water at 60-80degree Celsius with the use of solar water heaters. The following are the core benefits of the SWH:

• the significant benefit of SWH is the fuel savings, such as the 100 liters of SWH can efficiently work as an electric geyser for any residential purpose. It can easily save 100 units of electricity per year which is relatively cost-effective.
• The SWHs are also effective for power generation and minimizes the cost substantially. For instance, using 1000 numbers of 100-liter capacity SWH can easily save 1MW of power.
• There are numerous environmental benefits; by using the SWH as a 100litres capacity, SWH can quickly reduce 1.5 tonnes of carbon dioxide per year.
• The payback period for SWH is quite ample as these are equipped with a life span of 15-20 yrs. The payback period for the same is 3-4 years, and it can be pretty efficient throughout its lifetime.

DIY for Common Problems in Solar Water Heater

There are numerous households where SWH is a common name. Apart from the household, these are also used for different industrial applications.

• For household purposes, some of the problems lie in SWH that are mere and can be effectively catered to by simple DIY tactics.
• The following are the problem faced and the probable cause of the same:

Water not available in the hot water tap

This is among the general problems that come in SWH due to the no cold water supply or the wear and tear in the valve at the outlet of the system closed.

• One of the major causes can be the Airlock in the pipes.
• This can be catered by cleaning and proper greasing of the pipes.

Heating does not happen at all

Here is no proper heating of the water then it must be due to several reasons such as high consumption of hot water. It can be catered by using checkpoints and using patterns.

• In this, the collector may be shaded that helps in the heating of the water appropriately. 
• Choking out of the piping system due to the scaling of dirt can be a prominent issue.

Enough heating of water is not attained

This is one of the problems that are pretty common in the news; this occurs due to the cloudy weather the high consumption of hot water.

• One of the core reasons also is the frequent switching on and off of the hot water tap.
• This also causes wear and tear of the mechanism.
• Apart from this, the collector should be checked for dirt; partial choking of the collector can also cause this problem.

Quantity of water received is low

This is among the problems that can be caused due to the vapor locking in the collector and the pinching of the inlet or outlet pipes. This can be catered to by proper checking and dirt cleaning.

• With the bove DIY solutions, it is pretty easy to cater to all the problems related to the SWH that are likely to be generated after usage.
• One can DIY easily as these are not that complicated ones.

Conclusion

One of the essential equipment which has a vivid need in almost every household needs innovative approach. Using solar energy to fulfill the demand for hot water is among the best approach. It does reduce not only the carbon footprint but also provides long-term savings. With this equipment, everyone is doing their bit of work towards mother nature by reducing their share of pollution. With this excerpt, it is clear that the SWH can be of ultimate use with minimal energy obtained by using fossil fuels. Here we have also discussed the core work as well as different kinds of SWH. In addition to that, it also has some of the common problems that can easily be catered through the solution provided. However, there is much more to learn about solar energy-driven types of equipment, but getting the idea of SWH is pretty efficient. We will try to cover other aspects of solar energy in the next set of articles.