In this article, we will learn the moment of inertia of a triangle, along with examples, calculation, etc. Let’s explore!
What is Moment of Inertia of Triangle? Definition
Let’s try to understand the moment of inertia of triangle basics. Some of the basics of the moment of inertia of a triangle are stated below.
- Moment of inertia of the triangle can be discussed and stated in three major aspects. First is the passage of the axis via the centroid. The second is the passage of the line through the base. The third is the axis perpendicular to the base.
- The moment of inertia of any shape, including triangle with respect to non-centroidal, and an arbitrary axis can be determined if the moment of inertia of the centroidal axis, which is parallel to the first one, is already known. In this scenario, we use the parallel axes theorem.
The parallel axis theorem is commonly used to find the moment of inertia of composite sections.
How to Express Moment of Inertia of a Triangle?
The expression of the Moment of inertia of a triangle can be given in numerous ways and it depends on the the location of axis. The moment of inertia of the triangle is different for the different locations of the axis. There square measure sometimes 3 moments that may be thought of. They are;
- Axis travelling through the mass’s centre.
- Axis passing through the bottom.
- The axis perpendicular to its base.
We will look into every expression below and later on we will calculate and know how to calculate the moment of inertia of the triangle.
01. Axis traveling through the mass’s centre
The moment of inertia of a triangle with its axis parallel to its base and traveling through the center of mass is stated as; I = bh3 /36; Here,
- b = base breadth and
- h = height
02. Axis passing through the bottom
The moment of inertia of a triangle is given as; if we have a tendency to take the axis that passes through the bottom: I = bh3 / 12
We can additionally use the parallel axis theorem to prove the expression wherever the Triangle center of mass is found or found at a distance capable of h/3 from the bottom.
03.The axis perpendicular to its base
Let’s try to see a triangle’s instant of inertia when its axis is perpendicular to its base, we must first consider that the axis y’-y’ is used to divide the whole triangle into two right triangles, A and B. These triangles, on the other hand, can have a standard base capable of h and heights b1 and b2. For each, the moment of inertia can be: Iy’ = hb13 / 12 + hb23 / 12
If we have a tendency to think about b2 = b – b1 wherever the parallel axis y-y through the center of mass is at a distance ⅔ ( b/2 – b1) from y’-y’ then we are able to simply realize or calculate the instant of inertia ly.
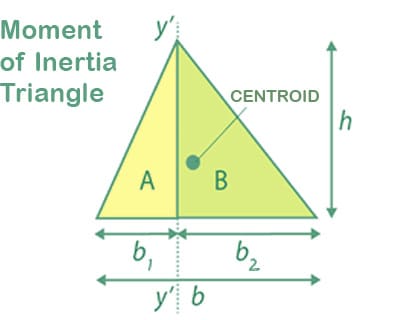
We are able to use the parallel axis theorem to try and do. Thus, In any case, once pure mathematics substitutions, we have a tendency to get the expression as: Iy’ = (hb / 36) (b2 – b1 b + b12)
How to Calculate Moment of Inertia of a Triangle?
We will take the case wherever we’ve got to see the instant of inertia concerning the center of mass y. We are going to take into account the instant of inertia y about the coordinate axis.
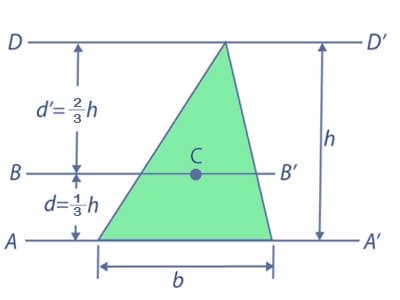
We can use the parallel axis theorem and that we will take the center of mass as a reference during this case. Here, IAA’ = IBB’ + Ad2
- IBB’ = IAA’ – Ad2
- IBB’ = (1/12) bh3 – 1/2 bh (1/3) h2
- IBB’ = bh3 / 36
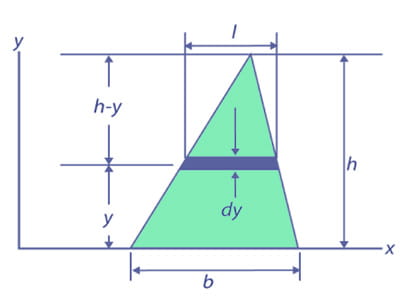
Next, we are going to realize the instant of inertia once the axis passes through its base:
- dlx = y2 dA
- dA = l dy
If we have a tendency to take similar triangles we are going to have,
- (l / b) = (h – y) / h
- l = b (h – y )/ h
- dA = b [(h – y) / h]dy
Now we are going to integrate dlx from y = zero to y = h.
- Ix = ∫ y2 dy
- Ix = 0∫h y2 b (h – y)/ h
- Ix = b/h 0∫h (hy2 – y3)
- Ix = (b/h)[h (y3/ 3)- (y4 / 4) ]0h
Therefore, Ix = bh3 / 12.
Moment of Inertia of Triangle Solved Problem or Calculation
Question#1 Calculating the moment of inertia of an equilateral triangle
Problem: An equilateral triangle is formed when 3 rods having mass “m” and length “l” are joined together. Determine the moment of inertia of the system about an axis passing through its center of mass and is perpendicular to the triangle’s plane.
Solution: The moment of inertia of rod BC is given by: I1= ml2/ 12
From the parallel axis theorem, the moment of inertia of the required rod is:
- I2= I1+ mr2 = ml2 / 12 + m ( 1/ 2 √3)2 = ml2/ 6
Since the triangle is made up of three rods, hence the moment of inertia of all three rods is given by:
- I = 3I2
- I = 3 (ml2 /6)
- I = ml2/2
Question#2 Calculating product of inertia of right-angle triangle with respect to 2 cases
Problem: Determine the product of inertia of the right triangle 1) with respect to x and y axes 2) with respect to centroidal axes parallel to the x and y axes.
Case-1
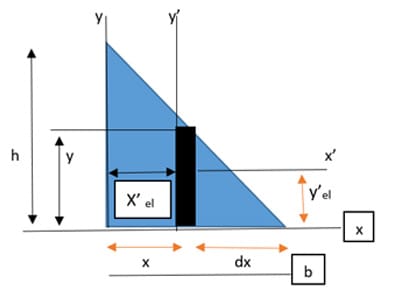
Case-2
Solution: Case-1: Finding the product of inertia by directly integrating with the parallel axis theorem on vertical differential area strips.
Y= h(1- x/b) d A= ydx = h (1- x/b) dx
X’ el = x y’ el= ½ y= ½ h= (1-x/b)
Now, integrating d I x from x= 0 to x= b
Ixy= ∫ d Ixy = ∫ X’ el y’ el d A = b 0 ∫ x (1/2) h2 (1-x/b)2 dx
= h2 b0 ∫ (x/2 – x2/b + x3/2b2) dx= h 2( x2/ 4 – x3/3b + x4/ 8b2)b0
Ixy= 1/24 b2 h2
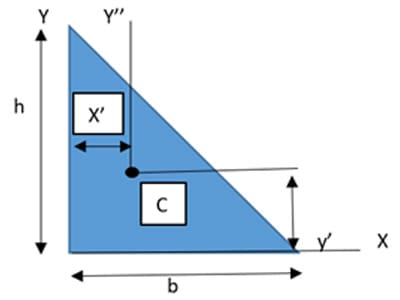
Case-2: We will apply the parallel axis theorem to determine the product of inertia with respect to centroidal axes.
X’= 1/3 b y’= 1/3 h
From case 1:
Ixy= I’ x’’ y’’ + xy’ A
I’x’’ y’’= 1/24 b2 h2 – (1/3 b) (1/3 h) (1/2 bh) = -1/72 b2 h2
Conclusion
Hence, we have learned the basics of the MI of a triangle and how to calculate this value along with sample calculation. Any questions in mind, please let us know in the comment section!


The thing i like about your blog is that you always post direct to the point info.:,*`,