What is the second law of thermodynamics? Any idea! So in this article, we will be learning all about the second law, its definition, examples, equation or formula, applications, and how it answers the questions of the universe expansion and its unprecedented end! Let’s begin.
What is the Second Law of Thermodynamics?
Let’s try to understand the basics of the second law of thermodynamics. In the previous blog, we studied all about the first law of thermodynamics its use, and applications. This law is unable to specify,
- In which direction the energy will transfer?
- Energy quality
In Layman’s language, if we take a metallic rod of uniform temperature, the first law cannot specify whether this uniform temperature will become hotter at one side and cooler at opposite sides spontaneously. Thus, the limitations in the first law need to be fulfilled by another principle or law. Hence, the second law of thermodynamics is introduced.
Second of Thermodynamics Statement
The second law of thermodynamics states that, For a spontaneous process, the overall entropy change of a system plus its surroundings will always increase.
Second of Thermodynamics Explanation
Let’s try to understand the meaning of the second law. It simply tells that, if you keep a system isolated, over the its entropy that means the measure of disorder of that system will increase. We will understand this statement with a detailed explanation as well as examples.
Why Does the Second Law of Thermodynamics Require?
The energy flow from one system to another in the form of heat or work. But no limit has been set on the amount of total energy of a system that can flow out as work by the first law of thermodynamics. This drawback is covered by the second law of thermodynamics which states that the flow of heat will flow from the energy reservoir at a higher temperature to the reservoir at a lower temperature and vice versa without external assistance.
- This statement is critical in comprehending the operation of heat engines, which operate between two energy reservoirs running at different temperatures.
- The first law of thermodynamics establishes a relationship between the amount of heat used and the quantity of mechanical work generated but doesn’t specify the conditions under which the heat and work conversion will take place and also the heat transfer direction is not specified.
- The second law of thermodynamics bridges the gap between these discrepancies.
Heat Engines and Reverse Heat Engines Performance Evaluation
- A system that converts thermal energy into mechanical energy by bringing working substances from a higher temperature state to a lower temperature state which then can be used to perform mechanical work is known as heat engines.
- Internal combustion engines, thermal power plants are some of the examples of heat engines.
- A heat engine tries to extract maximum work output from a given positive heat input, the measure of this success is called the thermal efficiency of the engine which is given by,
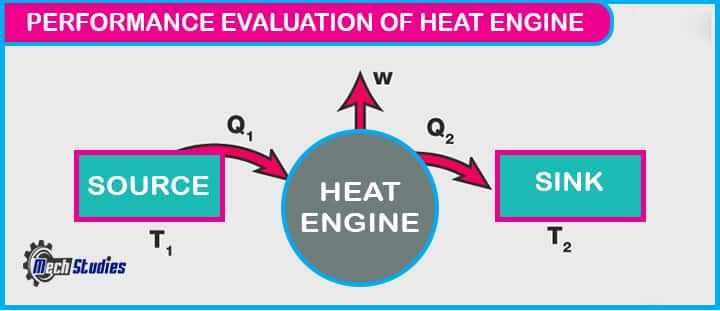
Thermal efficiency, ηth = W/Q1
Where,
Q1 = Heat input to the engine
W = Network output from the engine
- The reverse heat engine is used when work is done on a system to move energy from a lower temperature object to a higher temperature object.
- A reverse heat engine tries to extract maximum heat from the cold reservoir by providing maximum work input into the pump, this success is measured by the coefficient of performance (C.O.P), which is given by,
Co-efficient of performance, (C.O.P)Heat pump = Q1/W
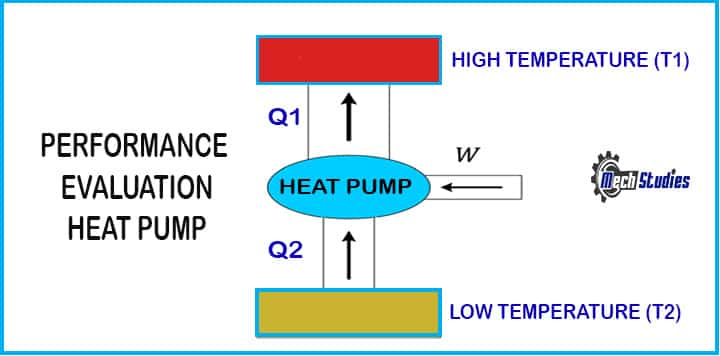
Where,
- Q1 = Heat output from the pump to a heat reservoir
- W = Network input to the pump
Above equations give the relation Q1 – Q2 = W, it can be used to simplify the equations for thermal efficiency and coefficient of performance by using heat transfer (Q) as a variable.
- ηth = (Q1 – Q2)/Q1
- (C.O.P)REF = Q2/(Q1 – Q2)
- (C.O.P)Heat pump = Q1/(Q1 – Q2)
The thermal efficiency is always less than unity and the coefficient of performance for a heat pump is always greater than 1.
Expression of the Second Law of Thermodynamics through Various Statements
Clausius statement
It is impossible to build a self-acting device that continually transfers heat from a low-temperature energy reservoir to a higher-temperature energy reservoir without the assistance of external work.

Simply it means, heat cannot flow from a cold body to a hot body itself.
Kelvin – Planck statement
It is impossible to build an engine that, when running in a cycle, creates no other effect other than extracting heat from a single reservoir and performing the same amount of work. Clausius’s statement and kelvin – Plancks statement for heat transfer are different but they are equivalent due to the fact that the violation of any one implies the violation of other.
Kelvin-Planck and Clausius statements equivalence
The Clausius and Kelvin-Planck versions of the second law are identical. This equivalence can be established by demonstrating that violating one proposition can result in a violation of the other. If a device is pumping heat Q1 from an energy reservoir at low temperature T1 to an energy reservoir at higher temperature T2 without the aid of any external work this will violate the Clausius statement and this arrangement is impossible.
- Now let’s consider a similar arrangement between the same reservoir at temperatures T1 and T2 and the heat input to engine Q2 at temperature T2.
- It will convert a small amount of heat into work and transfer the remaining energy to the reservoir as Q3.
- But since the above arrangement is transferring similar energy from Q1 to Q2 this will eliminate the need for a reservoir at heat engine input.
- Heat output from the pump can directly be transferred to the heat engine input.
This arrangement will create a machine that will produce continuous work with a single reservoir. Thus, violating the kelvin-Planck statement.
PMM2 – Perpetual Motion Machine of the Second Kind
When a machine produces continuous work output by absorbing heat from a single thermal reservoir. The heat absorbed is completely converted to work, such machine is known as the perpetual motion machine of the second kind – PMM 2.
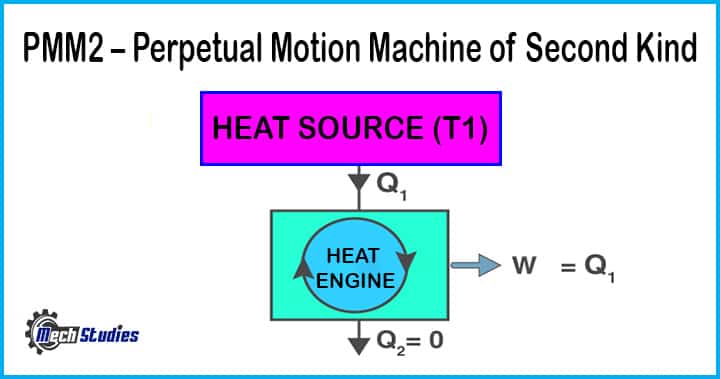
This machine eventually violates the second law of thermodynamics.
Fun fact
- The ammonia motor designed by John Gamgee in the 1880s was the prototype machine that was made to mimic the perpetual motion machine of the second kind. The heat reservoir of an ammonia motor is filled with ammonia, at -33° C, ammonia boils. It would evaporate at room temperature, creating a vapor pressure of 4 atm that would power a piston. The vapor would cool, condense, and return to the reservoir for the next cycle as it expanded.
- This machine is impossible as it violates the second law of thermodynamics, It is impossible to transmit heat from a colder to a hotter body. Thus the ammonia must be cooled by refrigeration to condense it before sending it for evaporation again which will consume more energy than the engine’s output.
Clausius Inequality
- When a reversible engine has more than two reservoirs, the third or higher-numbered reservoirs will not have the same temperature as the first two. Consideration of the formula for engine efficiency suggests that for optimal efficiency, all heat transfer should occur at maximum or minimum reservoir temperatures.
- Using an intermediate reservoir will result in the lowering of the efficiency of the heat engine. Engines used in practical applications witness a continuous change of temperature during a heat transfer process.
- The optimal way for a cycle with constantly changing temperatures is to imagine the system to be in communication with a large number of reservoirs in motion. Each reservoir is thought to have a temperature that differs by a little amount from the one before it. In such a scenario, each reservoir might be replaced by a reversible heat engine communicating with conventional reservoirs at the same temperature T0.
- The system to which heat transfer is applied is unconcerned about the source of energy or the mechanism of transmission, except that it must be reversible. Work transfer dW is associated with the heat transfer dQ in the original system, and the first law applied to this system is given by –
- ∑ (dQ – dW) = 0
- Applying the second law to the new system by replacing the engine reservoir. Positive work transfer is not achievable with a single reservoir if the new system is not a perpetual motion machine of the second kind.
- ∑ (dQ – dW) ≤ 0
- By considering the thermodynamic temperature we get,
- dW/dQ = (dQ0 – dQ) = (T0 – T)/T
Combining the above equations we get,
T0 ∑ (dQ/T) ≤ 0
Since T0 ≠ 0,
∑ (dQ/T) ≤ 0
This is called as Clausius Inequality.
Carnot cycle
- Sadi Carnot, a French engineer, proposed a reversible engine cycle known as the Carnot cycle in 1824.
- Any fluid may be used to power the Carnot cycle. Heat flows into the cylinder when a high temperature energy source is applied to the cylinder head during expansion, and heat flows out of the cylinder when a lower temperature energy source is applied to the head during compression.
Assumptions of Carnot engine
The assumptions of the Carnot engine are as follows,
- The motion of the piston inside the cylinder does not develop any friction.
- The piston and cylinder wall is considered to be perfect insulators.
- The cylinder head is designed in such a way that it may be either a perfect conductor or a perfect insulator of heat.
- The temperature of the source or sink is not affected by heat transfer.
- An ideal gas with constant specific heat is used as the working medium
- Compression and expansion are reversible processes.
Carnot cycle completes in four stages
Let’s see all stages in Carnot cycle,
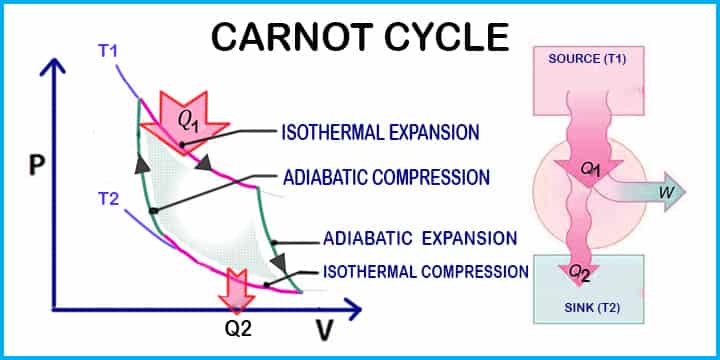
Stage 1:
A hot energy source is used through which the fluid absorbs heat Q1 while expanding isothermally and reversibly at a constant high-temperature T1.
Stage 2:
The cylinder becomes a perfect insulator, and no heat flow occurs. While the temperature declines from T1 to T2, the fluid expands adiabatically and reversibly.
Stage 3:
A cold energy source is used in which the heat Q2 escapes from the fluid while it is isothermally and reversibly compressed at a constant lower temperature T2.
Stage 4:
The cylinder head becomes a perfect insulator, preventing heat flow. The compression is sustained adiabatically and reversibly, with the temperature rising from T2 to T1. The enclosed area of the cycle represents the work delivered from the system during the cycle. Thus by applying the first law of thermodynamics the total work done is equal to the difference between the heat supplied Q1 at source and the heat rejected Q2 at the sink.
W = Q1 – Q2
Carnot cycle is an ideal system and cannot be performed in practice due to the following reasons:
- Having a frictionless process is impossible
- Heat transfer without temperature potential is impossible
- Isothermal processes can only be done if the piston travels slowly enough to enable heat transfer and keep the temperature constant.
- The adiabatic process can only be done if the piston travels as quickly as possible such that heat transfer is minimized owing to the limited time available.
- Since the isothermal and adiabatic processes occur during the same stroke, the piston must travel slowly for a portion of the stroke and quickly for the remainder of the stroke. This variance in piston motion during the same stroke is impossible.
Carnot’s theorem and its corollary
- It states that any engine operating between the given constant temperatures of source and sink cannot have an efficiency greater than the reversible engine.
- Its corollary states that – If all the reversible heat engines are operating between the same temperature levels then their efficiency is the same.
Carnot cycle consists of four working processes among which two are isothermal processes and two adiabatic processes. We can understand the system by considering a piston and cylinder arrangement –
- When the heat is added to the cylinder the gas expands resulting in the movement of the piston from one position to another and when the heat is rejected from the cylinder the piston moves down and gas is compressed.
- This heat addition, gas expansion, heat rejection, and the compression of gas is combined into four processes for a Carnot cycle.
Four processes in the Carnot cycle
1. Isothermal expansion or constant temperature process
- In isothermal expansion, heat is absorbed continuously from the heat source by the gas. So Qin is absorbed in temperature T1.
- During the process, the pressure of a gas is slightly decreased and the volume increases. The temperature of the gas remains constant and entropy increases.
2. Adiabatic expansion or constant entropy process:
- In the adiabatic process, the gas will not absorb or reject the heat. Here the expansion of gas takes place, pushing the piston upward.
- There’s a sudden decrease in the pressure and an increase in the volume of gas. There’s a decrease in temperature and the entropy remains constant.
3. Isothermal compression or constant temperature process:
- In the isothermal compression process rejection of heat takes place Qo, the piston moves down to compress the gas while the temperature remains constant.
- The compression results in an increase in pressure and a decrease in the volume of gas. The temperature of the gas remains constant and entropy will be decreased.
4. Adiabatic compression or constant entropy process:
- In adiabatic compression, heat is neither added nor removed from the system and the compression of gas takes place until the gas is compressed and the piston reaches its initial state.
- During compression, the pressure is increased and the volume of gas is decreased. The temperature of the gas is increased and the entropy remains constant.
The efficiency of Carnot cycle
The efficiency of the Carnot cycle is given by the ratio of net work done by the system to the heat added to the system. The work done by the system is given by the difference between the heat added to the system and heat rejected from the system, thus the efficiency is given by:
η = W/Q1
η = (Q1 – Q2)/Q1
In terms of temperature, the efficiency of the Carnot engine is given by the temperature difference of reservoirs at higher and lower temperatures,
η = 1 – (T2/T1)
Carnot Cycle’s Limitation
- It is a theoretical concept. Being an ideal cycle Carnot cycle does not exist and hence cannot be built.
- In Carnot cycle, there’s heat addition in the isothermal process but this is not possible as it will increase the temperature eventually scrapping the isothermal process.
- Maximum efficiency is possible in the Carnot engine as it does not consider the losses and frictions, in practice such high efficiency is not possible.
Conclusion
Hence, we have got a basic idea about the second law of thermodynamics along with its basics. Any questions, please let us know.

