Stress and strain is explained along with definition, formula, or equations, a lot of examples. Let’s explore stress & strain!
What is Stress and Strain? Definition
Stress and Strain Basic Concept
Take a body, and apply some external force on it. What will happen? Will the body be same after the application of force or its size or shape will be changed? Yes! Its size or shape will be different from the original body, basically there will be a deformation. Its length or diameter may be changed.
- If external force is more, then naturally deformation will be more.
- If external force is less, deformation will be less.
It is understood that the deformation depends on the force. But how this deformation happens and why?
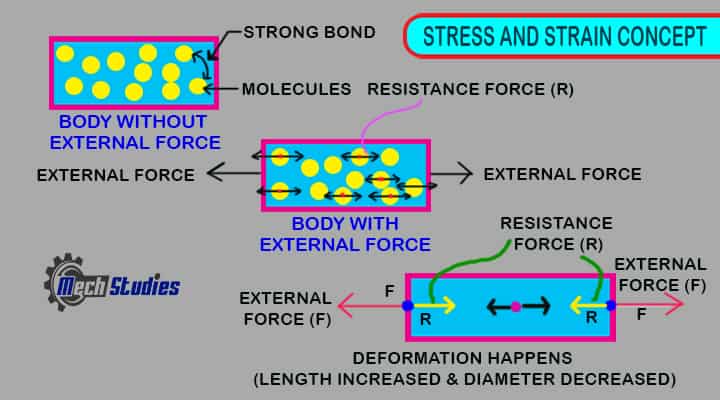
Let’s try to understand! Each body is consisting myriads of molecules and there are cohesive forces in between. When we apply external force on the body, the body will try to resist this external force by its own cohesive forces. This force is internal and acts as a resisting force to the external force.
Now, when we talk about resisting for per unit area or deformation with respect to the original dimension, stress and strain come into the subject.
Stress Definition
It is a type of resisting force that acts on a body per unit area. When this resisting force is exerted by the body to avoid deformation, is known as stress.
- The force that acts on the body is called load or force.
- The difference in load and stress is, the load is applied to the body by external means, and stress is induced in the body on behalf of the material, body made up.
- A loaded body will remain in equilibrium until the resisting force, generated by the body against deformation is equal to the load is applied to the body.
Stress = Force/Area
Strain Definition
Strain is induced in the body when it is subjected to any external force or load. This external load changes the original dimension of the body, so the strain is the ratio of change in dimension to the original dimension.
Strain = Change in dimension / Original dimension
Now it’s clear that strain is dimensionless or unitless.
Equation or Formula of Stress Strain
Formula of Stress
Based on the definition, if we apply force on a body, it will be stretched or compressed based on the application. Stress means force that is applied per unit area. It is generally represented by σ (Sigma) and written as,
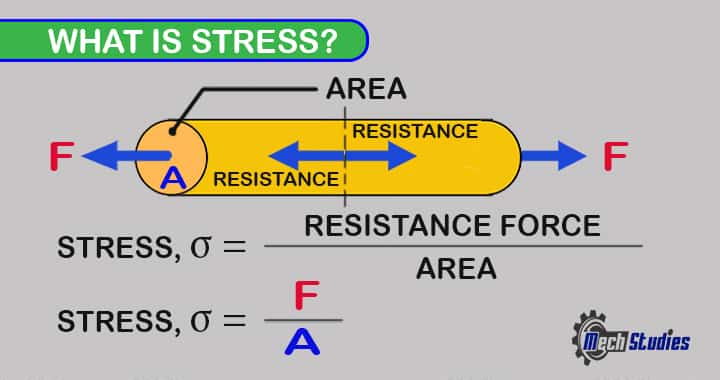
σ = Forced / Area
σ=F/A
Where,
- σ = Stress due to application of force
- F = The value of applied force to the body
- A = The area where the force is applied
Stress is written as force/area, hence, the unit of stress is N/m2
Formula of Strain
We have seen that due to the application of force, there will be deformation. Now, this can be,
- length-wise or may be
- lateral.
As per the definition of strain, it is simply the ratio of deformation in the direction of the application of force to the original dimension.
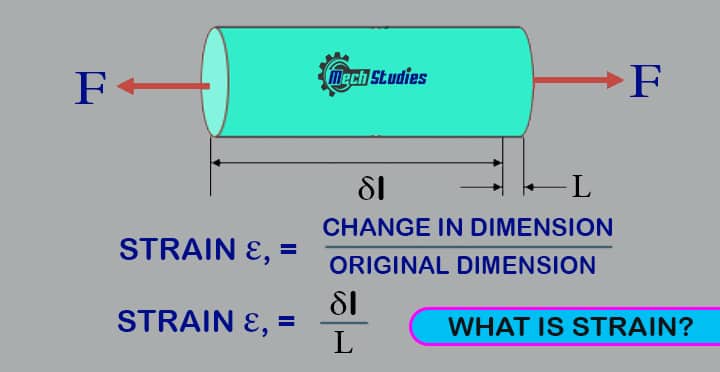
The strain can be represented, as follows,
ϵ=δl/L
Where,
- ϵ: Strain due to the deformation or by the stress
- δl: Change in dimension, say length-wise
- L: Initial length of the body.
Stress-Strain Relationship
We have got the basic definition, as well as equations or formulas for stress and strain. Now, what is the relationship between stress and strain? Any idea! This relationship is stated by law, named Hooke’s law! Let’s see Hooke’s law and stress-strain relation! As per this law, Stress is proportional to Strain.
That means, Stress ∝ Strain
- σ ∝ ε
- σ = E x ε
- E = σ / ε
- E = (F / A) / (dl / lo)
Where
- F = Applied force (N)
- A = area (m2)
- dl = Change in length (m)
- lo = Original length
- E = Young’s Modulus (N/m2)
Types of Stress and Strain
Type of Stress
Stress is differentiated into two types, for better understanding the meaning of stress,
- Normal stress
- Shear stress
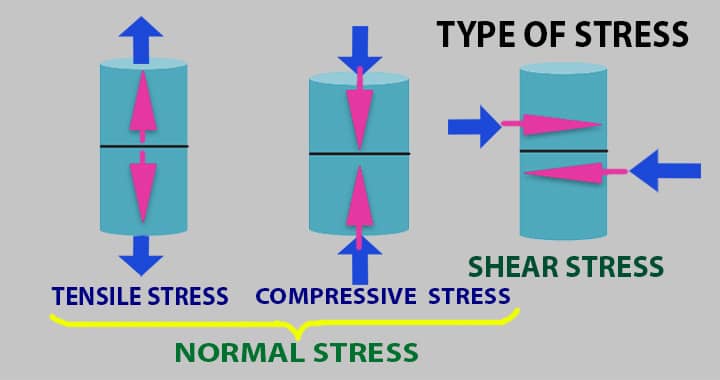
Normal Stress
Normal stress is further divided into the following types – tensile stress, and compressive stress.
Tensile stress
Tensile stress arises, when two equal and opposite forces act on the body in different direction.
- The tensile stress results in, increase in the length of the body.
- The ratio of increase in length and original length is called as tensile strain.
- So tensile stress acts normal to the area and pull out the area of the body.
If force F (pulling force) is applied on a body of cross-sectional area A to stretch it, and ‘R’ is the resisting force, then, from the definition of stress, We can write,
- Tensile stress, σ = Resisting force/cross-sectional area (R/A)
- Tensile stress, σ = External force (Pulling)/ cross-sectional area (F/A)
- Tensile stress, σ = F/A [as Resisting force, R = External force, F]
σ = R/A = F/A
Compressive stress
Compressive stress induced in a body when it is subjected to two equal and opposite forces acts in same direction of the body. Compressive stress results decrement in the length of the body. If force F (pushing force) is applied on a body of cross-sectional area A to compress it, and ‘R’ is the resisting force, then, from the definition of stress, We can write,
- Compressive stress, σ = Resisting force/cross-sectional area (R/A)
- Compressive stress, σ = External force (Pushing)/ cross-sectional area (F/A)
- Compressive stress, σ = F/A [as Resisting force, R = External force, F]
σ = R/A = F/A
Shear stress
This type of stress arises in a body when it is subjected to two equal and opposite forces tangentially across the section, where resisting force is acting.
- Due to this force, the body becomes shear from the resisting section area, known as shear stress.
- The corresponding strain of this stress called shear strain.
So we can say that shear stress is a type of stress that act tangentially to the area of the body. It is denoted by ‘𝜏’
A body consists of two parts and kept one over another. If force F is applied on both the parts on opposite directions, a resisting force, or technically termed as shear force, R will be created at the adjacent area. So, from the definition of stress, We can write,
- Shear stress, 𝜏 = Resisting or shear force (Shear resistance)/shear area (R/A)
- Shear stress, 𝜏 = External force/shear area
- Shear stress, 𝜏 = F/A [as Shear force, R = External force, F]
𝜏 = R/A = F/A
Thermal stress: Thermal stress is the result of change in temperature within the body. Thermal stress induced in the body when temperature is getting raised or lowered and also the body is not free to expand or contract. On the other hand, if the body is free to expand or contract, no stress will induce in the body.
Types of Strain
Strain is divided into four types –
- Tensile strain
- Compressive strain
- Volumetric strain
- Shear strain
- Longitudinal strain
- Lateral strain
Tensile strain
When a body is subjected to external load and it results change only length of the body then the ratio of increase of length of the body to original length of the body is known as tensile strain.
Compressive strain
This strain is come into when two equal and opposite forces acts opposite in direction then this force decreases the length of the body, due to compression strain is arises which is known as compressive strain. It is ratio of decrease in length to original length of the body.
Volumetric Strain
Volumetric strain is the ratio of change in volume of the body to original volume(before application of the force) of the body.
Shear strain
Shear strain is induced in the body due to shear stress. The force or load is considered in this strain will act tangentially.
Longitudinal strain
Longitudinal strain is defined as the ratio of axial deformation of the body to original length of the body. When a body is loaded with axial load or force then it’s length will increase and other dimensions of the body at right angle to the force applied will decrease. This type of deformation right angle to the body is called lateral deformation.
Lateral strain
The strain arises right angle to the force applied on the body, known as lateral strain.
Principle Stress and Strain
Stress which acts on principle plane, is known as principle stress. Principle plane is defined as the plane which does not consist shear stress. So, Principle stress has only normal stress and zero shear stress.
Mohr circle
Mohr circle is a graphical method to find out the normal, tangential and resultant stress on the oblique plane. Mohr circle comes into consideration when a body is subjected to two mutual perpendicular principal stresses, which are unique and unlike.
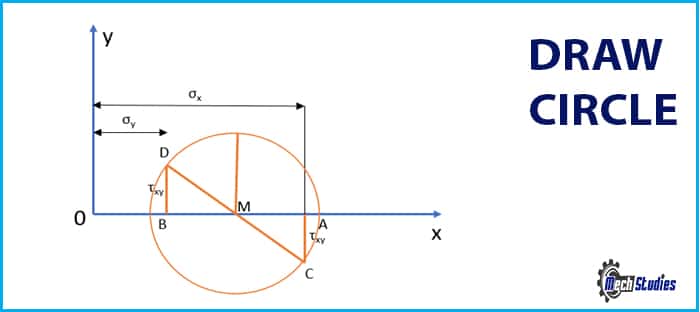
Mohr circle method is used for some special cases when –
- A body is subjected to two mutual perpendicular principle tensile stress of unequal intensity.
- A body is subjected to two mutual perpendicular principle stress, are different. I.e. one is tensile and other one is compressive stress.
- A body is subjected to two mutual perpendicular tensile stress accompanied by simple shear stress.
Strain Energy
It is type of energy which induced in a body in stained condition. So it can be said that the energy stored in body through straining effect, known as strain energy.
Straining effect can be produced by gradual applied, sudden applied load or impact loading. This indicates that, any kind of load is capable to produce straining effect. Strain energy is depends upon the work done by the force applied on the body and the strain energy is equal to the work done by the work done through load applied in deformation of the body.
Terms related to Strain Energy
Resilience
Resilience is a strain energy stored in a body due to straining effect i.e. It is total stored strain energy in a body due to straining effect and when this force is removed body must be capable to do some work so it can be said that resilience is capacity of stained body for doing some work on removal of straining force.
Proof resilience
Proof resilience is defined as the capacity of Max stored strain energy in a body, when it is stressed up to elastic limit. Hence proof resilience is quantity of strain energy stored in a body which is strained up to the elastic limit.
Modulus of resilience
It is important property of the material, which directly depends on proof resilience. Modulus of resilience is directly proportional to the proof resilience and inversely proportional to the volume of the body. Hence, in short it is proof resilience per unit area.
Modulus of resilience = proof resilience/volume of the body
Shear Stresses in Beam
Bending stress can be produced only if there is zero shear force, which results in zero shear stress in the body. So to produce bending stress in a beam, a part of this beam subjected to constant bending moment and zero shear force then the induced stress in the beam will come out as bending stress. Note that, there will be no other stress within the beam.
In bending stress, the reason of no shear stress is there, shear stress is equal to shear force divided by area. Therefore shear stress is directly proportional to the shear force. Hence in bending stress shear force is zero, in result shear stress is also zero.
- In actual application bending moment varies from section to section, when it is applied on the beam.
- It is also note down that in actual practice, shear stress acting on beam will not be completely zero. There must be some shear force present and varies from section to section.
- So if there is shear force then some shear stress must be arise in beam.
- This shear stress act across transverse section of the beam.
- Here complimentary horizontal shear will be produced due to presence of transverse shear stress. This complimentary horizontal shear stress act at longitudinal layer of the beam.
Direct Stress
Direct stress individually produced in a beam, when beam is subjected to an axial tensile or compressive load. In a body, bending stress can be produced only if there is bending moment. To produce both bending stress as well as direct stress. Body has to subject to axial load and also bending moment too.
Bending Stress in Beam
Shear force and bending moment are set up at every section of the beam by applying some external load. Because of the shear force and bending the beam undergoes to some deformation.
- It is very difficult to measure the stresses but with certain assumptions, these stresses(shear and bending stress) can be measured.
- The stresses induced from the bending moment, known as bending stress.
Pure Bending
Pure bending defined when a length of beam in subjected to constant bending moment with zero shear force, then stresses will be arises in the length of the beam due to bending moment only, known as bending stress and the length of the beam said to be in pure bending or simple bending. It should be noted that there will be only bending stress and because of zero shear force, shear stress is zero.
A point load on simple supported beam produces pure bending. Assumption used in simple bending. In theory of simple bending, some assumption are made, which must be take into consideration before moving to simple bending theory –
- The beam taken for experiment, their material should be homogenous and isotropic.
- In tension and compression the value of young’s modulus of elasticity is same.
- The transverse section of the beam is plane before bending and also after bending.
- Considered beam is straight at initial condition and all longitudinal filaments tending to the circular arc with common centre of curvature.
- Radius of curvature is greater than the dimension of cross section.
- Every layer of the beam should be free to each other, so that they can freely expand or contract, i.e. layers are independent from below are above of it.
Theory of Simple Bending
In the below Fig. 6, a part of the beam is subjected to simple bending. Consider a small length dx of this beam. Now consider two-section AB and CD, which are normal to the axis of the beam N-N.
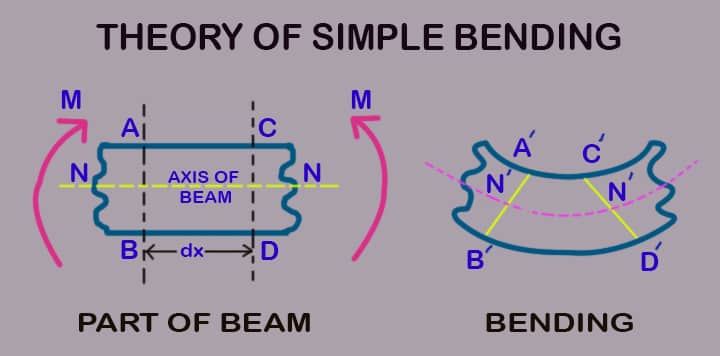
Because of bending force, the bending moment will induce, as result dx will deform as in above Fig. 6 seen. This deformed fig clear that all the layer of beam, which were originally same before deformation, do not remain same in length any more. Let the top layer is named as AC will deform to A’C’ shape. This deformed layer has become shortened in its length.
Take bottom layer as BD deformed to B’D’. This layer is longer than the original layer BD. So we can say that from fig(2), some of the layers have been shortened while some elongated between the top and bottom layers. Some layers neither shortened nor elongated, they are neutral in position and known as a neutral layer or neutral surface.
Fig. 5 has section N’- N’, the line of intersection of neutral layer on the cross-section of beam known as the neutral axis. The layer above N – N axis or N’ – N’ axis becomes shortened and below this axis elongated.
The above layer of N-N axis become decreased due to compressive stress. The increase in the layer below N – N axis is due to the application of tensile stress.
Fig. 6 shows that the top layer shortened maximum and as well as we move forward to N – N section the decrease in length become decreases. At the exact N – N section, there is no change in length so it defines that compressive stress is maximum at top of the layer. In respect of this tensile stress will be maximum at bottom layer.
When we move from bottom layer to N – N section. The increase in length decreases respectively. Hence the amount by which layer increase or decrease in length, depends upon the layer with respect to N – N. This theory of bending is known as theory of simple bending.
Difference Between Stress and Strain
What is the difference between stress and strain? Let’s look at these differences in a table,
| S.no | Stress | Strain |
| 1 | Stress means the amount of resisting force per unit area. | Strain means change in dimension by original dimension. |
| 2 | Stress is represented by the Greek letter sigma ‘σ’ | Strain is represented by the symbol Epsilon ‘ε’. |
| 3 | Theoretically, stress is written by, Stress = force/area | Theoretically, strain is written by, Strain = change in length or diameter/original length or diameter |
| 4 | The formula or equation of stress is given by σ=F/A | The formula or equation of strain is given by ϵ=δl/L |
| 5 | Stress has unit and it is N/m2 (S.I unit) | The strain doesn’t have any unit. |
| 6 | Stress is existed normally in tensile, compressive and shear stress forms | Strain exists in Tensile, Compressive, Volumetric, Shear, Longitudinal & Lateral strain forms |
| 7 | Stress can exist even there is no strain | Strain never exists in absence of stress. |
| 8 | Stress cannot measure directly with use of any kinds of instruments. | Strain can be measure directly with the help of strain gauge |
| 9 | Stress comes after strain | Strain comes fast |
After the difference between stress and strain, you may wonder that stress and strain both are force by area and both have the same unit, then how can we differentiate? Let’s see the differences.
Difference Between Pressure vs Stress
The difference pressure and stress shall be, as follows,
| Sr. No | Pressure | Stress |
| 1 | When we apply an external force on a body, it is simply defined as the ratio of that external force per unit area. | When we apply an external force on a body, it is simply defined as the ratio of that internal resistance force per unit area. |
| 2 | Represented by ‘p’ normally | Represented by ‘σ’ |
| 3 | Pressure cannot act in any direction or any angle, it always acts normal to the surface where it is acting. | Stress can act in any direction or any angle, and it is not limited to normal direction. |
| 4 | If pressure is applied, stress can be produced | If stress is applied, pressure will not be developed |
| 5 | Pressure means it always intends to compresses things. | Stress means it can be compressed or tensile or even shearing |
| 6 | Pressure means external | Stress means internal resistance |
| 7 | Pressure is applicable for solids as well as liquids | Stress is applicable for solids only |
| 8 | It is a thermodynamic property | It is a material property |
| 9 | The value of pressure is always positive and we used to write, Pressure = (+) F/A | Stress can be either positive as well as negative and it can be, Stress = (–) F/A or (+) F/A |
| 10 | Pressure can be measured directly with the help of instruments like barometers, manometers or pressure gauges | Stress cannot be measured directly with the help of any instruments. |
| 11 | Pressure is a scalar quantity as it doesn’t have any direction. Pressure at a point means it acts in all direction with a same magnitude | Stress is a vector quantity as it has different magnitude in different direction. |
| 12 | It doesn’t depend on the surface area | It totally depends on the surface area |
Conclusion
Hence, we have learned the basics of stress and strain, their definition, meaning, relationship, formula or equation, etc. Any doubt, please let us know.

Hi! Do you use Twitter? I’d like to follow you if that would be okay. I’m undoubtedly enjoying your blog and look forward to new posts.|
This page truly has all the information and facts I wanted concerning this subject and didn’t know who to ask. |
I really love your blog.. Great colors & theme. Did you build this web site yourself? Please reply back as I’m planning to create my own site and would like to learn where you got this from or just what the theme is named. Appreciate it!|
Hello Krysta,
Thank you for visiting us, its ACABADO theme.
Good article. I am going through many of these issues as well..|
I truly appreciate this post. I¦ve been looking all over for this! Thank goodness I found it on Bing. You’ve made my day! Thank you again