What is Viscosity? Water, Air, Oil – Definition, Meaning, Kinematic, Formula

In this article, we will learn what is viscosity, its type like kinematic viscosity, dynamic viscosity, value for water, air, oil, different formula, etc. Let’s explore!

What is Viscosity? Definition, Meaning

Viscosity Basics

Let’s try to understand the basics of viscosity. Processing materials relies heavily on fluid flow. Fluid means we understood liquid or gas. In most processes or industries, we have seen the various use of fluids, like,

• raw materials,
• reagents,
• many experiments, or
• heat transfer medium in heat exchangers,

Viscosity is a concept that is used not only in chemistry but also in physics and engineering.

• Often, viscosity is referred to as a fluid’s thickness.
• Water (low viscosity) and honey come to mind (high viscosity), In the case of fluids of differing densities, however, this definition can be a bit perplexing.

Viscosity Meaning

We’ve all seen two raindrops racing down a windshield, which is an example of viscosity in action.

• When a raindrop goes quicker, it is the one with the least viscosity (or resistance), which is why it wins.
• A high quantity of intermolecular friction causes a liquid or gas to be viscous.
• The more internal friction a liquid or gas has, the more viscosity it has, and the less it moves.

Viscosity Definition

Viscosity term came from the Latin word “viscum” and the meaning of “viscum” is viscous glue, basically a sticky thing. Viscosity is defined as a measure of a liquid or gas’s resistance to flowing or changing shape. In another way, viscosity is defined as, the ratio of fluid’s resistance to fluid flow.

• A fluid’s viscosity is a measure of its resistance to movement or evaporation. It’s a term used to describe the friction that occurs within a moving fluid.
• When fluid has a high viscosity, its molecular structure creates a lot of friction within the fluid, making it difficult to move. As a result of its molecular constitution, a fluid with low viscosity moves easily.
• When used in daily language, viscosity refers to “thickness” or internal friction. Honey has a higher viscosity than water, hence water is “thin.” Honey is thick. A fluid’s ability to move increases as its viscosity decreases (fluidity).
• Also, gases have a viscosity, but one that is tougher to detect under normal conditions.
• There are several applications for the viscosity law including inkjet printing, protein formulations, and injections, as well as food and beverage processing.

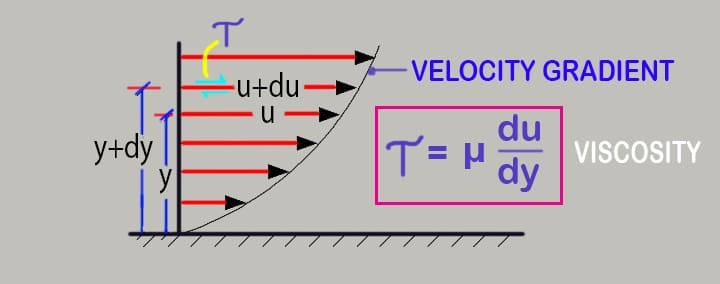
Shear Stress = 𝜏_yx = – μ du/dy

For this blog only let’s get into a greater aspect of what Viscosity actually is!

History of Viscosity

The discovery of viscosity is remarkable in that it was made three times independently by three distinct scientists, which makes it particularly interesting. Each of these experts discovered principles that have been combined to aid scientists today build new experiments and calculations.

• John-Louis-Marie Poiseuille and Gotthilf Hagen were the three men who molded viscosity into what it is today.
• John-Louis-Marie Poiseuille discovered viscosity in 1829 by testing the flow of liquids through a variety of thin tubes of varying sizes and shapes.
• For example, he discovered from this experiment that a liquid’s velocity depends on viscosity, provided that the tube’s length and diameter are constant. Poisesulle’s Law is the name given to this concept today, and it is employed in a variety of formulas and equations.

Types of Viscosity, Symbol

There are numerous sorts of viscosity. The maximum usually used withinside the area of fluid dynamics is shear or dynamic viscosity. However, relying on waft physics distinctive viscosities play corresponding essential roles. In totality, we can say there are three types of viscosity,

• Dynamic viscosity
• Kinematic viscosity
• Apparent viscosity

Before discussing all types of viscosity, let’s see the symbol first.

Symbol of Viscosity

• The symbol of Dynamic viscosity as μ,
• The symbol of Kinematic viscosity as η,

Let’s get into the types in brief!

Dynamic Viscosity

The shear or dynamic viscosity or viscosity is usually acquired with a speed profile experiment. Pictured here is one of many instances of a velocity profile, which is found in a boundary layer, for example, in which the wing is represented by the current flow of air:

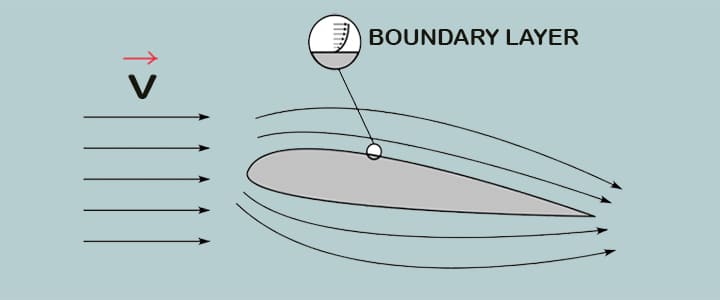
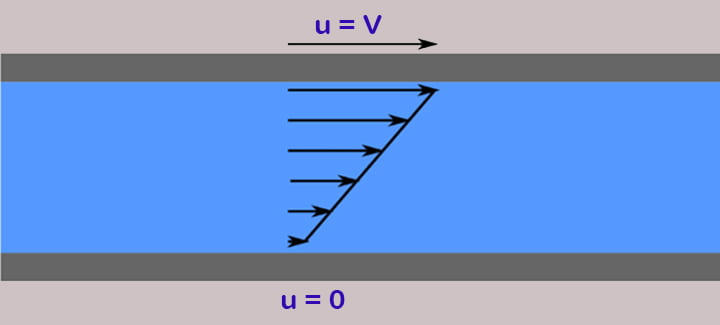
Most viscosity effects in body-fluid interactions occur at the boundary layer. As an example, two parallel plates with a non-zero relative tangential velocity are used in a renowned velocity profile experiment between the two plates, with no normal velocity. Let’s assume for the sake of simplicity that one plate is immobile and the second plate moves in the opposite direction at the same tangential velocity u=V. The fluid would then show a velocity profile.

This is because the fluid that is in contact with the fixed plate will have zero velocity and that which is contacting the moving plate will have the same velocity as it, namely V. This experiment can be seen in the picture below:

Kinematic Viscosity

When managing surprise waves and phenomena that consist of excessive and fast compression of the fluid, the majority viscosity η can’t be neglected, being associated with essential principles together with sound attenuation.

The kinematic viscosity ν=μ/ρ seems often in fluid mechanics and warmth switch and is associated with flows below the pressure of gravity. The Reynolds number, which connects the fluid’s momentum to its viscous forces, is one formulation that makes use of kinematic viscosity.

Apparent Viscosity

The viscosity of a Newtonian fluid is linearly proportional to the shear stress in a one-dimensional flow.

μ = 𝜏/(du/dy)

Where,

• τ = Shear stress acting on the fluid layer in contact with the moving plate.
•  du/dy = Variation in velocity in respect to height.

When it comes to non-Newtonian flow, the apparent viscosity ratio [𝜏 _{/ (du/dy})] may or may not be constant. The fluid type is determined by the relationship between the shear stress and the rate of deformation. A dilatant fluid is one that has an increase in apparent viscosity with the rate of deformation whereas the apparent viscosity of the pseudoplastic fluid is reduced as the deformation rate increases.

Viscosity Formula

Shearing stress to velocity gradient ratio is used to measure viscosity in a fluid. It is possible to determine the viscosity of a fluid using the following formula:

η = 2ga² Δρ/9v

Where,

• ∆ρ = Density between fluid and sphere
• a = Sphere Radius
• g = Acceleration due to gravity
• v = Velocity of Sphere.

Where,

v = Time taken to travel by the sphere.

• When calculating viscosity, the unit is Pascal seconds (Pa s). As you can see from this equation, the viscosity increases as the sphere’s speed decreases. Fluids that are thicker give more resistance to objects that move through them because of their viscosity.
• In spite of the fact that all liquids have a certain viscosity, the viscosity of water is often used as a standard.

We have already learned the other formula of viscosity,

Newtonian Vs Non-Newtonian Fluids differences

In general, Newtonian fluids have a fixed viscosity. Resistance increases as forces are increased, but it’s always proportional. A Newtonian fluid, on the other hand, behaves as a fluid regardless of how much force is applied to it.

• Inventor Isaac Newton believed that a fluid’s viscosity would remain constant independent of variations in the shear rate at a certain temperature and shear stress.
• He was partially correct. However, water and honey are among the rare examples of fluids that have such a characteristic behavior. Newtonian fluids are what we name them.
• But the viscosity of most fluids varies with the rate of shear. Non-Newtonian fluids are what they’re termed.
• The viscosity of non-Newtonian fluids, on the other hand, is not constant but varies widely depending on the force applied.
• Magnetorheological fluids are another class of non-Newtonian fluids. As a result of the magnetic field, they become practically solid but revert to their fluid condition when the magnetic force is removed
• Non-Newtonian fluids come in five varieties: dilatant, rheopectic, thixotropic, pseudo plastic, and plastic. The measurement of each of these fluids requires different considerations.

Viscosity Measurements

Viscosity is measured with different types of viscometers and rheometers. Fluids that can’t be described by their viscosity can be measured with the use of a rheometer, which requires more parameters than a viscometer.

• In materials like lubricants, whose viscosity can double with a shift of merely 5°C, precise temperature management is important. There are several fluids that have a constant viscosity regardless of shear rate (Newtonian fluids)
• They cannot be characterized by a single number since they do not have a constant viscosity (Non-Newtonian fluids). In non-Newtonian fluids, shear stress and shear rate are correlated in a variety of ways.
• In order to measure kinematic viscosity, glass capillary viscometers are commonly used.
• It is typical in the paint industry to measure viscosity with a Zahn cup, from which consumers receive the efflux time. Through the conversion formulae, the efflux time can also be translated into kinematic viscosities (centistokes, cSt).
• Viscosity is measured with the Stormer viscometer using load-based rotation. In Stormer viscometers, the viscosity is measured in Krebs units (KU).
• In a Ford viscosity cup, the liquid’s flow rate is measured. This is proportional to the kinematic viscosity under ideal conditions.
• When measuring viscosity, vibration viscometers can be employed. Vibration is used to evaluate viscosity in devices such as the Dynatrol, rather than rotation.
• Various rheometers that apply extensional stress can measure extensional viscosity. An acoustic rheometer can be used to measure the volume viscosity of a liquid or solid.
• The apparent viscosity of an oil or gas well drilling fluid is computed based on tests performed on it. All of this helps engineers build and maintain a drilling fluid that meets the specified parameters.

What are the Units of Viscosity?

We have already learned the definition and formula of viscosity, and we can write,

• μ = 𝜏/(du/dy)
• Viscosity or Dynamic Viscosity = Shear stress/Variation in velocity in respect to height

Let’s find out the units of viscosity!

Units of Dynamic Viscosity r viscosity = Units of Shear stress/Units of Variation in velocity in respect to height

Units of Kinematic Viscosity = Units of Dynamic Viscosity / Units of Density

Let’s try to understand SI, CGS units of viscosity in brief.

Dynamic Viscosity SI Units

So, SI Units of Viscosity = SI Units of Shear stress/SI Units of Variation in velocity in respect to height

• SI Units of Shear stress = N/m²
• SI Units of Variation in velocity in respect to height = (m/s)/m = 1/s

Hence, the unit shall be,

• or, SI Units of Viscosity = [ N/m²] /[1/s]
• or, SI Units of Viscosity = N-s/m²
• or, SI Units of Viscosity = N/m².s
• or, SI Units of Viscosity = Pa.s [as N/m² = Pascal or Pa]

Dynamic Viscosity CGS Units

So, CGS Units of Viscosity = CGS Units of Shear stress/CGS Units of Variation in velocity in respect to height

• CGS Units of Shear stress = dyne/cm²
• CGS Units of Variation in velocity in respect to height = (cm/s)/cm = 1/s

Hence, the unit shall be,

• or, CGS Units of Viscosity = [ dyne/cm²] /[1/s]
• or, CGS Units of Viscosity = dyne-s/cm²
• or, CGS Units of Viscosity = 1 poise [ as 1 poise = 1 dyne-s/cm²]

The name of the unit poise given is based on the name of French physiologist Jean Poiseuille.

Dynamic Viscosity SI vs CGS Units

CGS Units of Viscosity = dyne-s/cm² or poise

• SI Units of Viscosity = N-s/m²
• or, SI Units of Viscosity = 10⁵ dyne-s/10⁴ cm² [as 1 N = 10⁵ dyne and 1 m = 100 cm]
• or, SI Units of Viscosity = 10 dyne-s/cm²
• or, SI Units of Viscosity = 10 x 1 dyne-s/cm²
• or, SI Units of Viscosity = 10 x 1 poise

Kinematic Viscosity SI Units

S.I Units of Kinematic Viscosity = S.I Units of Dynamic Viscosity / S.I Units of Density

• S.I Units of Density = kg/m³
• S.I Units of Dynamic Viscosity = N-s/m²
• S.I Units of Dynamic Viscosity = [kg.m/s²]-s/m²
• S.I Units of Dynamic Viscosity = [kg./m.s]

Hence, the unit shall be,

• or, SI Units of Kinematic Viscosity = [ kg./ms] / [kg/m³]
• or, SI Units of Kinematic Viscosity = kg. m³/ms . kg
• or, SI Units of Kinematic Viscosity = m²/s

Dynamic Viscosity CGS Units

C.G.S Units of Kinematic Viscosity = C.G.S Units of Dynamic Viscosity / C.G.S Units of Density

• C.G.S Units of Density = gm/cm³
• C.G.S Units of Dynamic Viscosity = dyne-s/cm²
• C.G.S Units of Dynamic Viscosity = [gm.cm/s²]-s/cm²
• C.G.S Units of Dynamic Viscosity = [gm./cm.s]

Hence, the unit shall be,

• or, C.G.S Units of Kinematic Viscosity = [ gm./cm.s] / [gm/cm³]
• or, C.G.S Units of Kinematic Viscosity = gm. cm³/cm.s . gm
• or, C.G.S Units of Kinematic Viscosity = cm²/s = stroke [as 1 stroke = 1 cm²/s]

The name of the unit poise given is based on the name of Irish physicist George Stokes.

Kinematic Viscosity SI vs CGS Units

CGS Units of Kinematic Viscosity = cm²/s or stroke

• SI Units of Kinematic Viscosity = m²/s
• or, SI Units of Kinematic Viscosity = 10⁴ cm²/s or stroke [as 1 m = 10²]

Viscosity Solved Exercises & Calculations

Viscosity Calculation#1

A metallic plate of location 2.5 x 10^-4 m² is located on a 0.25 x 10-3 m2 thick layer of castor oil. If the pressure of 2.5 N is wanted to transport the plate with a pace of 3×10^-2 ms^-1, calculate the coefficient of viscosity of castor oil.

Given:

• A= 2.5 x 10^-4 m²,
• dx= 0.25 x 10^-3 m²,
• F=2.5N and
• dv = 3×10^-2 ms^-1

Calculate: Coefficient of viscosity of castor oil?

Solution: F = η A dv/dx

Hence, from this above equation, we can write,

• η = F/A . dx/dv
• η = 2.5 /2.5 x 10^-4 . 0.25 x 10^-3/3×10^-2
• η = 0.083 x 10^-3 Nm^-2s

Viscosity Calculation#2

A plate 0.1/2 mm remote from hard and fast plate actions at 60 cm/s and calls for a pressure of two N in line with meter rectangular to keep its speed. Determine fluid viscosity among the plates.

dy = 0.025 mm = 0.025 x 10^-3 m

Velocity of upper plate = 60 cm/s =0.6m/s

Force on upper plate = 2 N/m²

Shear stress = 2 N/m²

• du = change of velocity = u – 0 = 0.6 m/s
• dy = change of distance = 0.025 x 10^-3 m

Viscosity,

μ = 𝜏 / (du/dy) = 2/ (0.6/0.25 x 10^-3) =8.33 x 10^-5 P

Viscosity of Water, Air & Oil

Viscosity of Water

Let’s see the value of viscosity of water at different temperature. We will see the viscosity of water from 2⁰C, 4⁰C, 6⁰C, 8⁰C, 20⁰C, 80⁰C in centipoise or cP.

Temperature (°C)	Viscosity (mPa·s) of Water
2	1.6735
4	1.5673
6	1.4715
8	1.3847
10	1.3059
12	1.234
14	1.1683
16	1.1081
18	1.0526
20	1.0016
22	0.9544
24	0.9107
26	0.8701
28	0.8324
29	0.8145
30	0.7972
32	0.7644
33	0.7488
34	0.7337
36	0.705
37	0.6913
38	0.678
39	0.6652
45	0.5958
50	0.5465
60	0.466
65	0.4329
70	0.4035
80	0.354

Viscosity of Air

Like the viscosity of water, the viscosity of air also depends on temperature.

Temperature (°C)	Viscosity (mPa·s) of Air
0	0.01729
10	0.01778
20	0.01825
50	0.01963
100	0.02181
10	1.3059
12	1.234
14	1.1683
16	1.1081
18	1.0526
20	1.0016
22	0.9544
24	0.9107
26	0.8701
28	0.8324
29	0.8145
30	0.7972
32	0.7644
33	0.7488
34	0.7337
36	0.705
37	0.6913
38	0.678
39	0.6652
45	0.5958
50	0.5465
60	0.466
65	0.4329
70	0.4035
80	0.354

Viscosity of oil

Like the viscosity of water or air, the viscosity of oil also depends on temperature. An engine oil viscosity is tabulated as below,

Temperature (°C)	Viscosity (mPa·s) of Oil
0	1328.0
20	287.23
50	57.172
80	19.358

Importance of Viscosity

While viscosity may also appear of juvenile significance in each day life, it is able to absolutely be very vital in lots of one of kind fields. Examples of how viscosity measurements are utilized include the following:

Food Industries: In the food sector, viscosity measurements are utilized to enhance production profitability and efficiency. Because of this, it has an impact on how fast a product may be transported, how long it has taken to set or dry, and how long it would take to dispense liquids into packaging containers. The product’s viscosity must be taken into consideration when designing the production process, by making sure the pipes are slanted to maximize the flow of water, and the Dispensers need to be strong enough for flow, but not so strong that the package overflows. Also, food has a viscosity that can be described as a feature. Production must be closely monitored for viscosity assuring consistency between batches and will move smoothly through the production process.

Adhesives: We should think about how the adhesive will behave after it has been applied to a part when choosing the proper viscosity. Because of this, they will be easier to work with compared to the high-viscosity ones.

Vehicle Lubrication: When you place oil into your vehicle or truck, you ought to be aware of its viscosity. That’s due to the fact viscosity impacts friction, and friction, in turn, impacts warmth. In addition, viscosity additionally impacts the fee of oil intake and the benefit with which you’re automobile will begin in warm or bloodless conditions. Some oils have a greater solid viscosity, even as others react to warmth or bloodless; in case your oil’s viscosity index is low, it can emerge as thinner because it heats, which can motive troubles as you use your vehicle on a warm summer’s day.

Manufacturing: Manufacturing gadget calls for suitable lubrication to run smoothly. Too viscous lubricants can block and clog pipelines, hence they should be avoided. Lubricants that can be too skinny offer too little safety for shifting parts.

Pharma Industry: Viscosity may be of important significance in medication as fluids are added into the frame intravenously. Blood viscosity is a primary issue: blood that is too viscous can shape risky inner clots, even as the blood that is too skinny will now no longer clot; this may cause risky blood loss or even death. Other industries in which viscosity is important are Petroleum, Concrete, and Cosmetics.

Conclusion

So in this blog, we studied viscosity and its different aspects. While studying viscosity, we also focused on some other things like its units, formulae, and we understood how important is to identify the viscosity of different materials and the difference between them with respect to their viscosity. Happy reading.