What is Refrigeration Cycle? Basic, Components, Diagram & Explained in HVAC

The refrigeration cycle is the main basic cycle for all air conditioning and refrigeration equipment. In this chapter, we will discuss, the basics of a refrigeration cycle, mainly the vapor compression cycle, main concept, parts, components, working principle explained for HVAC system along with a real example, etc. Let’s get into the Refrigeration cycle!

What is Refrigeration Cycle? Basic & Definition

The refrigeration cycle is a thermodynamic cycle that generates refrigerating effects with the use of mainly an evaporator, compressor, condenser & expansion valve. This process is basically a thermodynamic process where the working fluid absorbs the heat from the surrounding at a low temperature and reject the heat to the atmosphere at a higher temperature.

• The refrigeration cycle is used to cool & heat or comfort design or as per process temperature requirements.
• It works based on reversed Rankine cycle.
• In this process, heat flows from low temperature to high temperature.

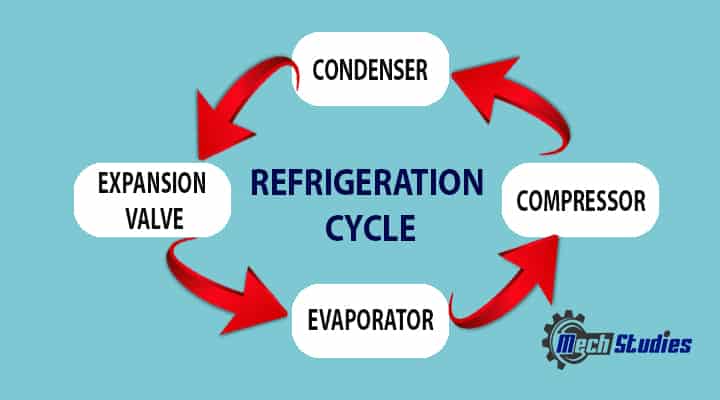
Refrigeration Cycle Basic Terms

There are a few concepts of refrigeration, which are necessary to know before discussing the refrigeration cycles.

• Evaporation
• Saturation Temperature
• Saturation Pressure
• Superheat
• Cooling
• Condensation
• Subcooling
• Change of boiling point with respect to pressure
• Heat Transfer

Would You Like to Know ‘How to Do Heat Load Calculation using HAP‘, you can check our course.

Our Course

Evaporation: Evaporation means a change of phase from liquid to gas. In this case, heat needs to be added for the change. The amount of heat required to evaporate a liquid is called heat of evaporation.

• It is measured at the liquid’s boiling point.
• If the boiling point is less, evaporation will be at less temperature.
• If the boiling point is high, evaporation will be at a high temperature.

Normally, the refrigerant has a very less temperature very less, for example, Refrigerant R410a has -51.7 deg. C. It means this refrigerant starts evaporating at normal atmospheric conditions. Now, what do you think about how this evaporation happens? It requires heat for evaporation and this heat comes from adjacent space. So, adjacent space or air or even water loses heat and becomes cool. How does cooling happens or how does HVAC works, is explained in a different article with a lot of images!

Saturation Temperature: It is nothing but the boiling point, basically, it means the temperature at which water boils into water vapor.

Saturation Pressure: It is nothing but the pressure at which water boils into water vapor corresponding to saturation temperature.

Superheat: Superheat, as the name suggests, means when heating is done in a little different manner, basically heats after vapor or saturation temperature. Let’s take some water & heat,

• We will see water will start boiling at 100 deg. C. and vapor will be formed.
• Heat more, the water temperature will not be increased (100 deg. C) but heat content will increase.
• If we add more heat, heat content, as well as the temperature of vapor, will increase, say 105 deg. C.

Here, the increase of temperature after the boiling temperature is called superheat.

• Superheat = Temperature at the current stage – Boiling Temperature
• Superheat = 105 – 100 = 5 deg. C

Cooling: We all feel cold in the winter season. But do you know why this cooling happens? What is the exact reason? Let’s try to understand with an example. Take a small amount of medicated spirit on your palm, and soon your palm will get cooled. How does the palm get cold? Steps are,

• We know that at normal pressure & temperature, the medicated spirit starts to evaporate.
• Now, the medicated spirit takes the heat from the palm.
• Palm loses heat
• We know, that losing heat means simply getting cold.

Condensation: Condensation means a change of phase from gas to liquid. In this case, heat needs to be rejected to change gas to liquid. If a refrigerant vapor rejects heat, at certain conditions, it will be changed into a liquid.

Subcooling: Subcooling, as the name suggests, means when cooling is done in a little different manner, basically cools below the temperature where the water vapor turns into liquid water. Cool the water –

• We will see water vapor will start to form a liquid at 0 deg. C.
• Cooling more, the water temperature will not be increased (0 deg. C) but cooling will be continued.
• If we cool more, heat content, as well as the temperature of the water, will decrease, say -2 deg. C.

Here, the decrease of temperature after the saturation temperature is called subcooling.

• Subcooling = Saturation Temperature –  Temperature at current stage
• Subcooling = 0 – (-2)  deg. C = 2 deg. C

Change of Boiling Point with respect to Pressure: Boiling a liquid at low pressure is easy. You will wonder when you will see water at normal pressure boiling at 100 deg. C but the same water at the mountain will be boiled at 80 deg. C. Why is this happening? It is because the pressure is less at the higher elevation and water boils at low pressure.

Heat Transfer: If you take an iron rod and heat one side of it holding the other side, very soon you will feel hot. Why does it happen? Because of heat transfer! Here, heat from the hotter section of the iron rod is transferred to the opposite side of the rod that was normal.

• So, heat transfers from a hot area to a cold area.
• But do you know when heat will flow from the hot to the cold region?
• or is it possible!

Yes, possible if we do some external work. Three ways i.e., conduction, convection & radiation are the method of heat transfer.

Refrigeration Cycle Description & Diagram

All refrigerating equipment & air conditioners work based on refrigeration cycles. We are discussing mainly the vapor compression cycle in this article. In another refrigeration cycle, namely vapor absorption is used in case of waste heat is available. It will be discussed in another article. Let’s learn, the basic description of the vapor compression type refrigeration cycle. Refrigerant circulates through evaporator, compressor, condenser, expansion valve and continues this cycle.

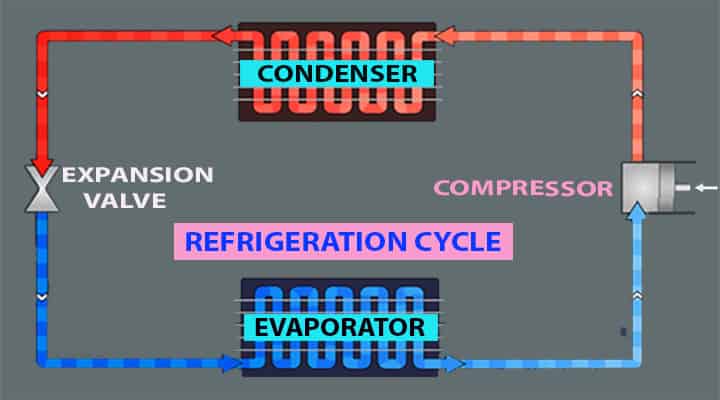
Components or Parts Name of Refrigeration Cycle

Now, let’s understand the parts of the components of a basic refrigeration cycle. Have you seen any inside view of our home split air conditioner during maintenance? Or have you visited any air conditioners repair shop? There are various kinds of refrigeration machines or air conditioners, but the basic refrigeration cycle has a basic cycle. Let’s try to explore the different components of a refrigeration cycle along with a brief explanation as well as the functions of each part. There are four (4) major components in air conditioners or refrigeration machine:

• Evaporator
• Compressor
• Condenser
• Expansion valve

Along with the main components, all other parts of the refrigeration cycle are

• Evaporator fan
• Filters
• Refrigerant
• Condenser fan
• Electric motors
• Controls
• Electrical cables
• Control cables
• Refrigerant pipes
• Drainpipes

Description of Refrigeration Cycle Components

Let’s start to learn the main parts of the refrigeration cycle,

Evaporator

The evaporator is one of the main equipment in the refrigeration cycle. It is nothing but a cooling coil that works as a heat exchanger in the refrigeration cycle.  

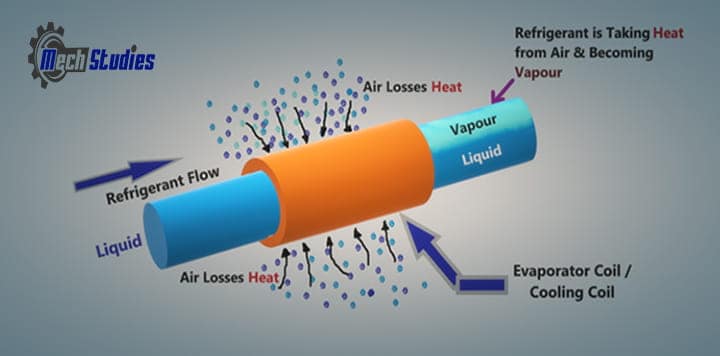
The main functions of the evaporator are,

• In the evaporator, the refrigerant changes its phase from liquid to vapor at normal pressure & temperature.
• To change this phase, the refrigerant needs heat, i.e. latent heat of vaporization.
• This heat comes from adjacent medium i.e. air or liquid, based on the system.
• Medium loses heat so, the medium is cooled.

The continuous phase change process occurs, and cooling effects are going on so that air conditioning is maintained. This evaporator is installed in an indoor unit, or air handling unit, or the indoor side of packaged air conditioners. The capacity of refrigeration units or air conditioners is based on the nos. or sizes of evaporator coils. If the capacity is more, the evaporator size will be more.

Compressor

The compressor, the most important part of the refrigeration cycle. It is mainly the heart of the refrigeration system. The main functions of the compressor are:

• Due to the rotation of the compressor, a low pressure is created at the suction side.
• Low pressure helps the water vapor to get into the compressor.
• It also helps to have a low pressure inside the evaporator.
• Continuous recirculation is maintained.
• The compressor compresses the vapor.
• In the compressor, the refrigerant vapor pressure & temperature is increased and a continuous pressure & temperature difference between the evaporator & compressor is maintained.
• This difference increases the speed of phase change from liquid to vapor and helps the refrigeration process faster.

After the compressor, the refrigerant goes to the third important component condenser.

Condenser

As the name suggests, the condenser simply condenses the refrigerant. It is a heat exchanger and it rejects heat from the refrigerant to the atmosphere. In the condenser, vapor changes into liquid by undergoing a phase change.

• Superheated refrigerant vapor is released from the compressor.
• In the condenser, heat content from the refrigerant vapor is reduced & becomes saturated vapor.
• Further reduction of heat content from the saturated vapor changes its phase from vapor to liquid.
• In this phase change, a slight low pressure or vacuum is created in the condenser which helps the condensation faster.
• The condenser is designed considering more surface area with fins arrangement which increases capacity.
• There are condenser fans to reject the heat from the refrigerant to the atmosphere.

Expansion Valve

The expansion valve is placed after the condenser and before the evaporator. The main function shall be as follows,

• It maintains constant pressure and temperature
• It controls the flow of refrigerant from the condenser to the evaporator
• This expansion valve reduces the high-pressure liquid line to low pressure in the evaporator.

Refrigerants

Refrigerant is the main working fluid in the refrigeration cycle. There are a few main characteristics of refrigerant by which it is selected. Normally, the following refrigerants are widely used in various refrigeration industries:

• R134a
• R410a
• R407c

The selection of refrigerant is based on the following,

• Less ODP (Ozone depletion potential)
• Less GWP (Global Warming Potential)
• Mainly environmentally friendly.

How Does Refrigeration Cycle Work in HVAC? Working Principle

Let’s try to understand the working principle of the refrigeration cycle.

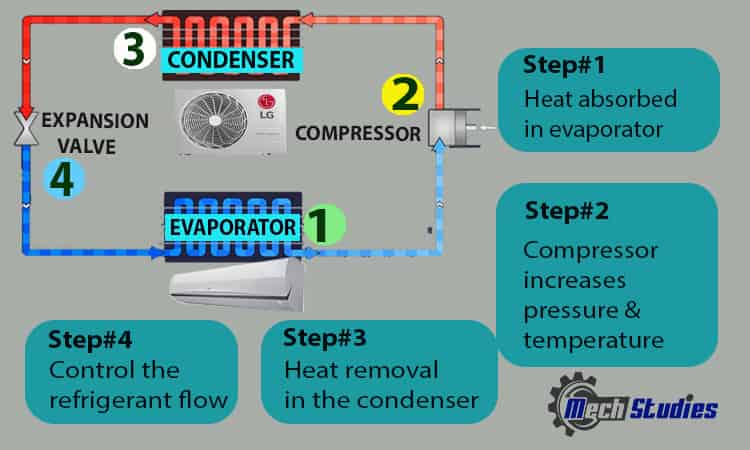
Step#1: Heat is being absorbed in the evaporator: We have already learned that refrigerant has a very low boiling temperature. So, normally, liquid refrigerant starts evaporating in the evaporator coil at normal pressure and temperature.

• The liquid refrigerant absorbs heat from adjacent spaces or mediums and changes its phase from liquid to vapor.
• If the adjacent medium is air, liquid refrigerant takes heat from the air and evaporation happens. By losing heat, the air gets cooled.
• On the other hand, refrigerant takes heat and becomes heated. At the outlet of the evaporator, all liquid refrigerant changed into vapor.

Step#2: Compressor increases pressure & temperature: When the power is on, the compressor is started to rotate. Due to this rotation, there will be a slight low pressure at the inlet of the compressor. Low pressure helps the refrigerant vapor to enter the compressor.

In the same way, the compressor compresses the vapor and increases pressure & temperature at the outlet. It creases a pressure gradient or pressure difference that forces the refrigerant vapor to enter the compressor.

Step#3: Heat removal in the condenser: After the compressor, refrigerant vapor with high pressure and temperature passes through the condenser. Here, the refrigerant vapor changes its phase from vapor to liquid and releases the heat into the sink or atmosphere.

Step#4: Flow control: At the outlet of condenser, liquid refrigerant along with vapor comes out but it needs to be,

• controlled as per requirements &
• entire vapor needs to be transferred into liquid.

These things are done in the expansion valve. This valve has a throttle device by which it controls the flow and due to the expansion effect pressure reduces. This reduction of pressure results in a phase change of vapor into liquid.

After the expansion valve, the mixture of liquid refrigerant & vapor is changed into liquid and it will enter to the evaporator. This refrigeration cycle continues and, in this way, the refrigeration system works. Refer to our ANIMATED VIDEO with simple explanation:

Working Principle Scheme of Refrigeration Cycle

It’s a very easy process and is explained step by step to have a clear understanding.

• Refrigerant is pumped in the refrigeration cycle or circuit.
• It is circulated through refrigerant pipes or tubing.
• It has a very low boiling point & it starts evaporating at normal conditions.
• The refrigerant present in the evaporator takes up the heat from adjacent air for evaporation.
• Refrigerant changed its phase from liquid to vapor.
• Low pressure is created at the inlet of the compressor.
• The compressor creates high pressure & temperature at discharge.
• The pressure differential between the inlet & outlet of the compressor sucks the refrigerant vapor from the evaporator.
• The condenser is the next component in the refrigerant cycle after the compressor.
• The refrigerant vapor is transferred to the next part of the refrigeration cycle to release heat into the atmosphere.
• After the condenser, the refrigerant travels to the expansion valve.
• The expansion valve controls the flow of refrigerant and refrigerant vapor present in the liquid refrigerant changed into a liquid.
• Then it goes to the evaporator and this refrigerant cycle continues.

A blower circulates air through the evaporator coil and cool air is transferred to the areas to be conditioned. In the same way, the condensing coil is also cooled by means of condenser fans.

Refrigeration Cycle T-S & p-h Diagram

 The refrigerant cycle is described by the T-S & p-h diagram.

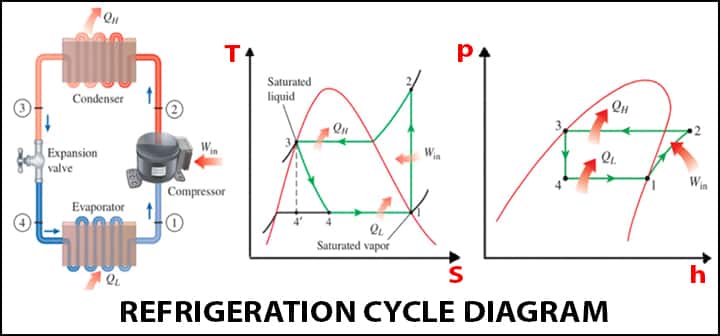
COP of Refrigeration Cycle

The efficiency of the refrigeration cycle is described by COP or coefficient of performance.

• h1 = Sp.  enthalpy before compression at Point 1
• h2 = Sp. enthalpy after compression at Point 2
• h3 = Sp. of enthalpy after cooling at Point 3
• h4 = Sp. enthalpy after expansion at Point 4

Hence, as per COP definition,

• COP = Refrigerating effect/Work-done
• COP = (h1-h4)/(h2-h1) 
• COP = (h1-h3)/(h2-h1) [As h3 is equal to h4]

How Does Actual Refrigeration Cycle is Different from Ideal Cycle?

The actual refrigeration cycle is different from the standard refrigeration cycle due to different losses:

• Vapor at the outlet of the evaporator is in superheated conditions.
• Superheated vapor prevents droplets of liquid refrigerant.
• There is a frictional force.
• Isentropic expansion doesn’t occur.
• The liquid refrigerant in the condenser is subcooled.
• Subcooled refrigerant helps to ensure 100% liquid entry to the expansion valve.
• A pressure drop occurs in the evaporator due to friction.
• A pressure drop occurs in the condenser due to friction.

Description of Actual Refrigeration Cycle & Diagram

Let’s try to understand, the actual refrigeration cycle or actual vapor compression cycle,

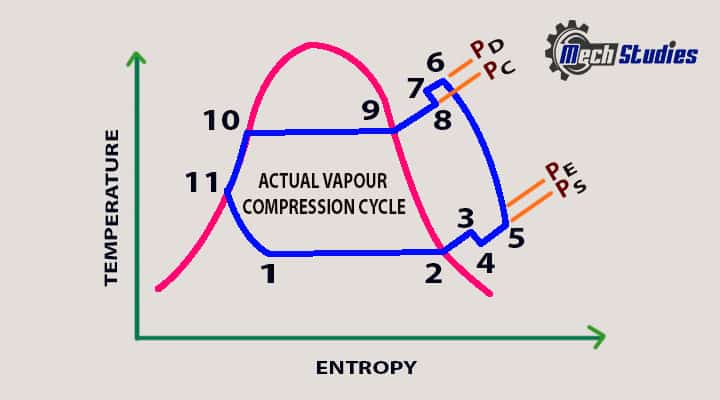
Process 1-2-3: The portion 1-2-3 indicates the flow of the refrigerant in the evaporator at suction pressure and temperature.

Process 3-4: This portion indicates a pressure drop as there is a resistance of the suction valve to the compressor.

Process 4-5: This portion of refrigeration cycle indicates the heat addition from the cylinder wall to the refrigerant.

Process 5-6: This portion indicates the actual process of compression of the refrigerant in the compressor.

Process 6-7: The portion 6-7 indicates cooling of the refrigerant at the outlet of the compressor.

Process 7-8: This part of the refrigeration cycle indicates a pressure drop due to discharge valve resistance.

Process 8-9–10-11: In this part, the refrigerant is desuperheated to dry state. Latent heat is removed and subcooling of refrigerant happens.

Process 11-1: This process indicates the throttling of sub-cooled refrigerant and in this portion, condenser pressure is changed into evaporator pressure.

Applications of Refrigeration Cycle

A simple application of the refrigeration cycle in our day-to-day life, you can see in the refrigerator. We get cooling with the help of the refrigeration cycle. Apart from the refrigerator, you can see many other applications of this cycle, as follows:

• Different types of air conditioning machines.
• District cooling system.
• Cold storage, etc.

FAQs for Refrigeration Cycle

What are the 4 cycles of refrigeration?

There are four cycles in a refrigeration cycle. These are
(1) Evaporation (2) Compression, (3) Condensation and (4) Expansion,

What is the cycle of refrigeration?

The refrigeration cycle is a cycle that has main four components: 
(1) Evaporator, (2) Compressor, (3) Condenser, (4) Expansion valve,
A Refrigerant is circulated in all the above components in a cyclic manner to get refrigerating effects.

How many types of refrigeration cycle are there? 

It is important to understand that the refrigeration cycle consists of four main components: the evaporator, the compressor, the condenser, and the metering device or thermal expansion valve. A refrigeration cycle has the main function of absorbing heat from indoor air and releasing it outdoors through a process called refrigerating.

Why is the compressor used in the refrigeration cycle?

As a result of the compression of the refrigerant, it becomes a high-pressure vapor, which becomes superheated as a result. After the refrigerant is compressed and heated, it leaves the compressor and enters the next stage of the cycle once it is ready to be used again.

What is a compressor in the refrigeration cycle? 

A compressor is the piece of equipment that increases the pressure of the working gas during the compression process. Compressors are one of the first steps in the refrigeration cycle. As low-pressure, low-temperature gas, refrigerant enters the compressor, and as high-pressure, high-temperature gas, it exits.

Which cycle is used in refrigeration?

The primary difference between a refrigerator and a heat pump is their purpose. 
As a result of reversing the Carnot cycle, it is possible for the heat and work interactions to be reversed. Refrigerators or heat pumps that operate on the reversed Carnot cycle are known as Carnot refrigerators or Carnot heat pumps.  

What is meant by the refrigeration cycle?

Often called a heat pump cycle, the refrigeration cycle routes heat away from an area that needs cooling. Compression and expansion are used to manipulate the pressure of the working refrigerant, such as air, water, or synthetic refrigerants.

In window air conditioners, what type of refrigeration cycle is used?

Due to the high temperature of the air, this process is referred to as the hot air cycle due to its high temperature. Following the cooling process of the refrigerant, the refrigerant is passed through the expansion valve and then enters the evaporator. Similarly, the hot air is mixed with the atmosphere, and then the fresh atmospheric air is blown over the condenser by the propeller fan, which absorbs the hot air and blows it over the condenser.

What is the refrigeration cycle in AC?

During the refrigeration cycle, an air conditioner uses a thermodynamic cycle. To absorb or release heat, it changes the pressure and state of the refrigerant. Heat is absorbed from inside your home and pumped outside by the refrigerant.

What are the steps in the refrigeration cycle?

The four steps that make up the refrigeration cycle are the compression process (compressor), condensation process (condenser), expansion process (expansion valve), and evaporation process (evaporator).

What is the hottest part of the refrigeration cycle?

There is a limit of 225 degrees Fahrenheit to the discharge temperature of any compressor. The system may start to fail if the discharge temperature reaches more than 225 degrees, which can happen as a result of worn rings, acid formations, and breakdown of the oil in the system.

What is the principle of refrigeration?

The principle of refrigeration is very simple! The cycle of refrigeration is used to remove the unwanted heat from a space to become desired design conditions. The equipment is used in this cycle, are capable to extract the heat and discharged it into some other place like atmosphere.
 In our home, we use air conditioner, where it conditions our rooms with its principle of refrigeration. Heat is removed from the room to make it condition and discharged into the atmosphere. A medium called refrigerant is used for heat transfer from room to outside with the help of its phase changes.

Conclusion

So, we have learned what is refrigeration cycle, how it works, diagram, etc., along with step by step working process explained. Any doubt, don’t hesitate to write to us!  Anyways, try to solve the quizzes to test the core of learning! Cheers! Happy Learning!