What is Pressure? – it’s a very common term in various industries. There are various kinds of pressure we use in our practical life. Atmospheric pressure, absolute pressure, gauge pressure, fluid pressure, units of pressure, conversions, etc. will explore here.
What is Pressure? Definition & Meaning
Pressure Basics
Let us try to understand the Pressure. Take a wooden block, a bowling pin, a sharp pin, and a hammer. Now, if you hammer on the bowling pin keeping on the block, do you think it will enter. No, it will not enter.
But about if you try to do the same thing on the sharp pin.
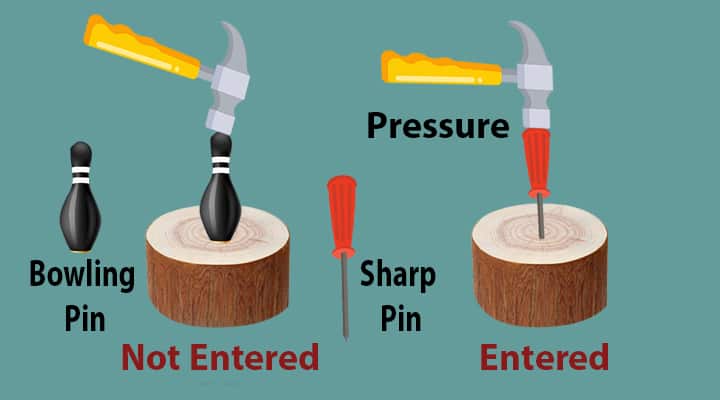
Don’t you think it will not enter? Yes, it will enter into the wall. Why this different behavior? Because of pressure!
Pressure Understanding
If we analyze, we will see the following two things:
1) Bowling pin- not able to enter into the wood
2) Sharp pin – easily able to enter the wood.
In both cases, we apply force on the head of the pin by the hammer. If apply the same amount of force, both the pins act differently.
What do you think, what may be the reason for this different behavior even the magnitude of the force is the same?
It is nothing but an area of application. The concept of pressure comes related to force and the area.
Pressure Definition
Hence, the are two factors that determine, whether pins will move into the wood or not,
- Magnitude of force
- Area of application.
The pressure is related to force and area and it is expressed as the amount of force applied per area. For the sharp nail, the area of application is very less and it moves and we say, the pressure is more. For a bowling pin, the area of a bowling pin is large, it will not be able to move and we say, the pressure is less.
Pressure Expression
Pressure can be defined as force per unit area which is applied perpendicular to the surface of the object. The mathematical equation for pressure can be written as:
P= F/A = mg/A
Where
- P : Pressure
- F : Normal force
- m : Mass
- g : Acceleration
- A : Area of the surface
Although the normal force is a vector quantity, the pressure is a scalar quantity (vector page).
Pressure Meaning
- The amount of force per unit area
- Force is applied perpendicular to the surface area
- The pressure is used to measure the amount of force acts in an area.
- Pressure depends on force and the area,
- If the area is small, the pressure is more.
- If the area is large, the pressure is less.
- Obeys pascal’s law
Units of Pressure & Conversions
S.I. Unit of Pressure
P = F/A
Now, the unit of P = Unit of Force (S.I Unit) / Unit of area (S.I Unit)
= N / m2 ((S.I. Unit)
This N/m2 is known as Pascal (pa). Hence, Pa is the unit of pressure in the S.I Unit.
1 Pa means 1 N force is applied in 1 m2 area.
Pa is applied for very small, normally kPa is used.
1 kPa = 1000 Pa = 1000 N/m2.
C.G.S Unit of Pressure
Now, unit of P = Unit of Force (C.G.S Unit) / Unit of area (C.G.S Unit)
= dyne / cm2 ((C.G.S Unit)
This dyn/cm2 is known as barye (Ba). Hence, Ba is the unit of pressure in the C.G.S Unit.
1 Ba means 1 dyn force is applied in 1 cm2 area.
F.P.S Unit of Pressure
Now, the unit of P = Unit of Force (F.P.S Unit) / Unit of area (F.P.S Unit)
= lbf / inch2 (F.P.S Unit)
This lbf/inch2 is known as pounds per square inch (psi). Hence, PSI is the unit of pressure in F.P.S Unit.
1 PSI means 1 lbf force is applied in 1 inch2 area.
Unit Conversions of Pressure
Bar to PSI or PSI to Bar
1 bar is equal to 14.5 psi
Let’s check few examples, from Bar to psi conversion or psi to bar conversions.
- 5 bar = 5 x 1 bar = 5 x 14.5 psi = 72.5 psi
- 7.5 bar = 7.5 x 1 bar = 7.5 x 14.5 psi = 108.75 psi
- 10.0 bar = 10.0 x 1 bar = 10 x 14.5 psi = 145 psi
- 100.0 bar = 100 x 1 bar = 100 x 14.5 psi = 1450 psi
In the same way, 14.5 psi is equal to 1 bar or 1 psi is equal to 1/14.5 bar
- 30 psi = 30 x 1 psi = 30 x 1/14.5 bar = 2.07 bar
- 60 psi = 60 x 1 psi = 60 x 1/14.5 bar = 4.14 bar
- 120 psi = 120 x 1 psi = 120 x 1/14.5 bar = 8.28 bar
Bar to Pascal/kPa & Pascal/kPa to Bar
1 bar is equal to 100000 pascal or 105 pascal or 100 kPa [1 kPa = 1000 Pa]
Let’s check few examples, from Bar to pascal conversion or pascal to bar conversions.
- 5 bar = 5 x 100000 pascal = 500000 pascal = 500 kPa
- 7.5 bar = 7.5 x 100000 pascal = 750000 pascal = 750 kPa
- 10.0 bar = 10 x 100000 pascal = 1000000 pascal = 1000 kPa
Pascal/kPa to PSI or PSI to Pascal/kPa
We have already seen that, 1 bar is equal to 14.5 psi and 1 bar is equal to 100000 pascal or 100 kPa [1 kPa = 1000 pascal]
Hence, we can say,
- 14.5 psi = 100000 pascal or 100 kPa or 1 psi = 100000/14.5 pascal and
- 100000 pascal = 14.5 psi or 1 pascal = 14.5/100000 psi
Let’s check few examples, from pascal/kPa to psi conversion or psi to pascal/kPa conversions.
- 5 psi = 5 x 1 psi = 5 x 100000/14.5 pascal = 34482 pascal = 34.482 kPa
- 7.5 psi = 7.5 x 1 psi = 7.5 x 100000/14.5 pascal = 51724 pascal = 51.724 kPa
- 10.0 psi = 10.0 x 1 psi = 10.0 x 100000/14.5 pascal = 68966 pascal = 68.966 kPa
- 12.0 psi = 12.0 x 1 psi = 12.0 x 100000/14.5 pascal = 82759 pascal = 82.759 kPa
In the same way, we have seen that 1 pascal = 14.5/100000 psi
- 1500 pascal =1500 x 1 pascal = 1500 x 14.5/100000 psi =0.218 bar
- 3000 pascal =3000 x 1 pascal = 3000 x 14.5/100000 psi =0.436 bar
- 5000 pascal =5000 x 1 pascal =5000 x 14.5/100000 psi =0.725 bar
Bar to Millibars/mbar or Millibars/mbar to Bar
1 bar is equal to1000 millibars
Let’s see few examples for bar to millibars conversion or millibars to bar conversions.
- 1.5 bar = 1.5 x 1 bar = 1.5 x 1000 millibars =1500 millibars or 1500 mbar
- 3.0 bar = 3.0 x 1000 millibars = 3000 millibars or 3000 mbar
- 2000 millibars = 2000 x 1/1000 = 2 bar
Pascal to Megapascal/MPa or Megapascal/MPa to Pascal
This Pascal to Megapascal/MPa or Megapascal/MPa to Pascal conversion is simple!
- 1 MPa = 106 pascal
- 1 pascal = 10-6 MPa
So, we can take few examples,
- 6 MPa = 6 x 106 pascal
- 9 pascal = 9 x 10-6 MPa
Pascal to hectopascal/hPa or hectopascal/hPa to Pascal
This Pascal to hectopascal/hPa or hectopascal/hPa to Pascal conversion is also simple!
- 1 hPa = 100 pascal
- 1 pascal = 1/100 hPa = 0.01 hPa
So, we can take few examples,
- 5 hPa = 5 x 1 hPa = 5 x 100 pascal = 500 pascal
- 200 pascal = 200 x 1 pascal = 200 x 0.01 hPa = 2 hPa
Types of Pressures
Pressures are different kinds and well discuss here in details,
- Atmospheric pressure or barometric pressure
- Vapour pressure,
- Absolute pressure,
- Gauge Pressure,
- Vacuum pressure,
- Differential pressure,
- Hydrostatic pressure or fluid pressure
- Bidirectional pressure,
- Static pressure,
- Dynamic pressure,
Atmospheric Pressure or Barometric Pressure
Air has pressure, and it will be understood if it can be kept in an enclosed area. Air exerted force on the wall of the surface. This atmospheric force per unit area is atmospheric pressure.
- It is normally written as atm
- The value of standard atm pressure is 101325 Pa or 101.325 kPa.
- It is equivalent to 760 mm Hg column
- In F.P.S unit, it is 14.7 psi.
- Its value depends on the elevation level.
- Atm pressure reduces with an increase in elevation.
Vapour Pressure
Vapor pressure is the pressure at a given temperature that is exerted by a gas in equilibrium with either a solid or liquid in a closed container.
- It is simply an indication of the evaporation rate of the liquid.
- If the temperature increases, vapor pressure will also increase.
Various units are used for vapor pressure:
- Pascals (Pa),
- atmospheres (atm),
- bar (bar),
- tor (mm Hg),
Absolute pressure
Absolute pressure is the pressure, measured with respect to perfect vacuum. There is no negative pressure below absolute pressure. The gauge pressure and atmospheric pressure together make the absolute pressure.
- It is expressed with ‘a’ like kPa(a) or psia
- Absolute pressure is always positive and below absolute pressure there is no negative pressure.
- It is the pressure that is measured relative to a complete vacuum.
- All absolute pressures above the complete vacuum is always positive.
- Absolute pressure is zero for a complete vacuum
- Absolute pressure will be never negative.
Gauge pressure
Gauge pressure is the pressure, measured with respect to zero atmospheric pressure. The difference between absolute pressure and atmospheric pressure is simply known as gauge pressure. We measure pressure with the help of a pressure gauge. The reading which we measure in the pressure gauge is called gauge pressure.
- It is normally expressed with a “g” such as in “kpa(g) or psig” etc.
- Gauge pressure consider ambient pressure as reference.
- It is simply absolute pressure minus atmospheric pressure.
- Gauge pressure in the vacuum area becomes negative.
Vacuum pressure
Vacuum pressure is just like the gage pressure, as it is measured with respect to atmospheric pressure, but it is measured below atmospheric pressure.
- This pressure is always negative.
Differential Pressure
Differential pressure means the difference between two pressures.
- It is commonly expressed with a “d” such as “psi(d)”.
- A differential pressure gauge is used to measure differential pressure.
- It senses gage pressure or vacuum pressure
Hydrostatic Pressure / Fluid Pressure
Hydrostatic pressure is the pressure that is produced by the hydrostatic force per unit area. If a liquid is kept in a container, the hydrostatic force acts at the base of the container.
This pressure is caused due to the gravitational force, which naturally pulls the fluid into the center of gravity of the earth that means downside.
- It is known as pressure head
- It is referred to as the height of the liquid
- It depends on the liquid density
- It doesn’t depend on the shape of the container.
- The pressure produced by a static fluid depends on the only depth of the fluid, density, and the acceleration of gravity.
The pressure (P) at any depth (ρ) is given by the equation:
- P = ρgh
Bidirectional Pressure
Bidirectional pressure is like gauge pressure with respect to atmospheric pressure.
- If it is measured above atmospheric pressure, it will be positive pressure
- If it is below atmospheric pressure, it will be negative pressure.
Negative Pressure
We have already learned that the lowest possible pressure is absolute zero pressure. Then how the term negative pressure comes?
But in the case of gauge pressure, both positive and negative pressure is possible.
- Actual negative pressure does not exist. Here, negative pressure means pressure, with respect to atmospheric pressure.
- If we say, -2 psi pressure, it means the pressure is 2 psi below the atm pressure. It can be written as 14.7-2 = 12.7 psi.
- This pressure is basically vacuum pressure.
- The lowest possible negative pressure is 14.7 psi.
Static Pressure
The Static pressure is the pressure which is measured when the fluid is at rest.
- Pressure when gravity is not considered.
- Pressure when motion is not considered.
We know, from Bernoulli’s equation:
If there will not be any change in elevation and fluid is static that is there will not be any flow, then the pressure will be static pressure.
The pressure p is the static pressure, with the above conditions.
Dynamic Pressure
Dynamic pressure refers to the pressure related to the fluid flow. It means the kinetic energy of the flowing fluid.
Pressure can be expressed as,
p = 1/2 γ v2
Where,
p= dynamic pressure, N/m2 (Pa),
γ = density of fluid (kg/m3)
v = velocity (m/s)
Diagram of Pressure
Absolute pressure, gauge pressure & atmospheric pressure relation
What’s the difference between absolute pressure and gauge pressure?
- The absolute pressure uses absolute zero pressure as its datum line.
- The gauge pressure uses atmospheric pressure as its datum line.
- The gauge pressure measurement is varied.
- The absolute pressure is definite and it will not be changed.
Absolute pressure = gauge pressure + atmospheric pressure
If you want to understand clearly you can watch an animated video to understand Absolute pressure, gauge pressure & atmospheric pressure and their relationship.
to understand Absolute pressure, gauge pressure & atmospheric pressure and their relationship.
Pressure Unit conversions Standards
The pressure is expressed in various units and there are certain standards for pressure units. These are as follows;
- BS350
- ISO31-3
- ISO 80000-4:2006
- PTB-Mitteilungen 100 3/90
- Perry’s Chemical Engineer’s Handbook, 6th ed, 1984
- SI system
Interesting Facts about Pressure
- The unit of pressure is pascal, we have already learned. It is as per French Mathematician Blaise Pascal.
- One atmospheric pressure = 101.325 pascal.
- Air pressure is measured by a barometer normally
- The weather forecast is dependent on air pressure.
- If low-pressure forms above the sea, there may be a chance of weather change or landfall or cyclone.
Don’t be Confused about Pressure & Pressure head
There is some little confusion between pressure and pressure head. So, how to differentiate between these two? It’s simple.
- Head means the height of the liquid column
- It is measured by the meter of the liquid column.
- It is expressed in m.l.c or meter.
- It doesn’t depend on the liquids.
Pressure, on the other hand, depends on the liquid. If density changes, the pressure will be changed.
The force of a fixed height liquid column will change over a unitary area with different specific liquids means different densities or specific gravities.
Hence, we can say, same height can generate different pressure. That means, the pressure head is the same but the pressure is different.
Water is generally used in the column as the most common liquid. But to measure the pressure in the small U-tube, heavier liquids need to be provided.
Normally, liquid mercury (Hg) is used as a heavier liquid than the water. Mercury is 13.6 times heavier than water. When you use the heavier liquid you don’t need to have that long column to measure higher pressure, so you can make a smaller and more convenient size column.
Water Pressure Calculation
Water pressure is one of the most familiar forms of pressure in day-to-day life.
The pressure is dependent on density, gravitational acceleration, and depth.
From Bernoulli’s equation, we can write,
P = ρgd
Where
- ρ = density of the liquid
- g = gravitational acceleration (g = 9.81 m/s2).
- d =depth
Let us solve a very small problem, to clear the doubt.
Given data,
- ρ = 1000 kg/m3, density of water at 22 °C,
- d = depth = 30m.
What will be the pressure?
Solution:
- P = ρgd
- ρ = 1000 kg/m3
- h = 30 m
- g = 9.81 m/s2
- P = ρgd
Hence, the value of pressure, P
- P = 1000 x 9.81 x 30
- P =294300 Pa
- P= 294.3 kPa
High Rated Course
Intro to Fluid Mechanics for Engineering Students Part 1
Intro to Fluid Mechanics for Engineering Students Part 2
Conclusion
We have learned the basics of pressure, along with its various types, like absolute pressure, atmospheric pressure, vacuum pressure, gauge pressure.
Do you any doubt, write to us. Thank you.
Check out to our a few interesting articles,
Reference Articles


I have learn several good stuff here. Certainly value bookmarking for revisiting. I surprise how much attempt you put to create one of these magnificent informative site.