What is Moment of Inertia of Rod? Calculation, Example

In this article, we will learn the Moment of inertia of Rod, along with examples, calculation, etc. Let’s explore!

What is Moment of Inertia of Rod?

Let’s try to understand the moment of inertia of rod basics.

Moment of Inertia Rod Basics

Let’s try to understand the moment of inertia of a rod. When a cylindrical rod is rotating, we are able to say if it’s in an angular motion, and that we want to calculate the precise point where the utmost mass is found, one can say or assume it’s going to be an axis of rotation from which the entire body is rotating.

But that’s where we are all wrong. It’s not compulsory to think that the mass element of a rod is often located at the center point or axis, and that’s where the moment of inertia of the rod comes into the image.

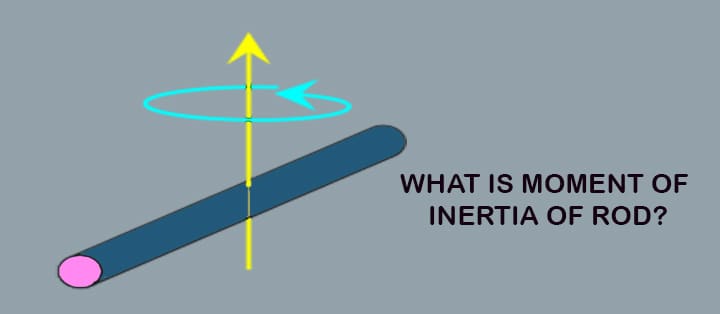
• Generally, when a rod is in angular motion, the mass elements of the item usually vary in an exceedingly different location from the center of the body.
• In technical words, the moment of inertia of rod is that the quantitative summation of the rotational inertia (motion) of the rod, i.e., the resistance applied by the rotational body within the front of torque which may be simply termed as turning force.
• The axis of rotation of a body will be external or internal, or we will assume it to be a constraint or a change. Although, the moment of inertia is often specified with the axis of rotation of a body in an exceedingly simpler condition.

Moment of Inertia of Rod Definition

The moment of inertia of a rod may be defined as the summation of the products which we get from the whole mass of every attached element of the rod and this whole then multiplying by the square of the particles with reference to its distance from the center.

• The moment of inertia of the rod which usually features a shape is often determined by using simpler mathematical formulae, and it’s commonly remarked as calculus.
• Within the case of the anonymous shapes of bodies, we are able to determine the instant of inertia by the experiments.
• One in every of the foremost commonly used experimental procedures incepted the relation between the time of rotation and therefore the mass of a suspended element.

Moment of Inertia of Rod – Axis through Centre

The Moment of inertia of a rod whose axis goes through the center of the rod, which features a mass (M) and length (L), is usually expressed as; I = (1/12) ML²

How to Derive Moment of Inertia of rod – Axis through Centre?

We have to remain in mind some things; we’ve to imagine that the rod is split into many pieces of infinitesimally thin slices. We’ve got to identify the variable to be summed. Within the first instance, the rod must be taken to possess an infinite number of point masses. All of their products are visiting be obtained by multiplying the square of the gap from the axis. We even need to contemplate the exceedingly small element of length dl corresponds to the mass dm.

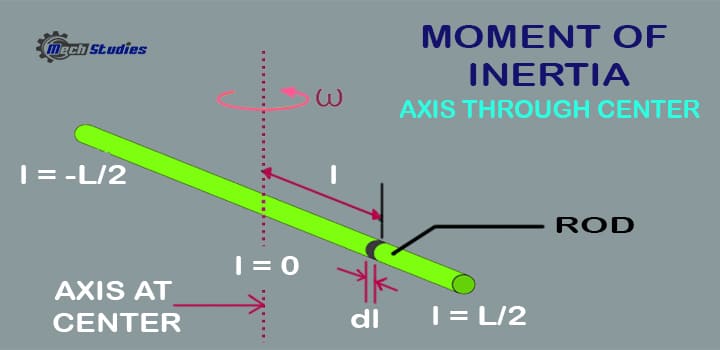
Besides, after we picture or label the origin at the center of mass that’s lying on the road of the axis, we’ll see that distance of the rod from the left is -L/2, while the gap from the origin to its right is +L/2. Now we’ve got to switch the worth of “dm” within the expression; Moment of Inertia of Rod:

•  I = _O∫^M l²dm

Now, as the rod is cylindrical and it is uniform, we can say its linear density is the same across its length.

• Linear density = Mass per unit length
• The linear density of rod (M/L) = Linear density of smallest part (dm/dl) [as density is same across the rod]

So, we can write,

• M/L = dm/dl
• or, dm = (M / L) dl

Moment of Inertia of Rod:

•  I = _O∫^M l²dm
• I = _-L/2 ∫^L/2 l² (M/L) dl [as dm = (M/L) dl ]
• I = M/L _-L/2 ∫^L/2 l² dl
• I = M / L [l³/3]_-L/2^L/2

Here the variable of the mixing is that the length (dl). The boundaries have changed from M to the desired fraction of L.

• I = M/3L, [(L/2)³ – (-L/2)³]
•  I = M/3L [L³/8 + L³/8]
• I = (M/3L) . 2L³/8
• I = (M/3L) . L³/4
• I = (1/12) ML²

Moment of Inertia of Rod – Axis through the End

When the axis of the rod passes through the best of the rod, another formula can be used to explain the Moment of Inertia. During this case, we use; I = ⅓ ML²

How to Derive Moment of Inertia of rod – Axis through Tip?

For calculating when the axis is at the top we’ve to draw the origin at that individual end. The same expression is often used but with another limit. Since the axis rests at the tip, the limit that’s utilized in integration is 0.

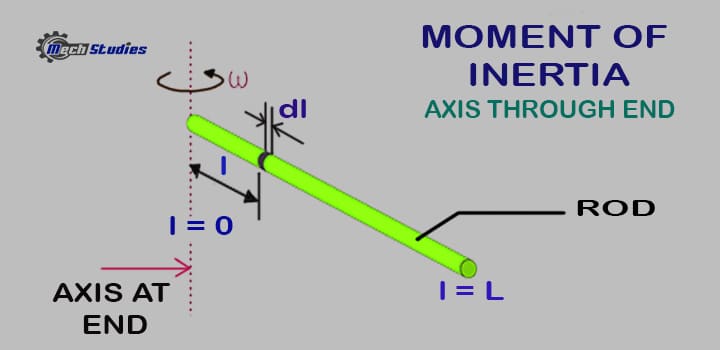
I = _O∫^M l²dm

I = _O∫^L l² (M/L) dl

If we apply the integration;

• L (end) = (M/L) _O∫^L l² dl
• L (end) = (M/L) [l³/3]₀^L
• L (end) = (M/3L) [(L³/3) – (/3)]
• I (end)  = (M/3L) [ L³ – 0³]
• L (end) = (⅓) ML²

Alternatively, the parallel axis theorem also can be accustomed to determine the expression. We have;

• Iparallel-axis=Icenter of mass+Md².
• I = L (cm) + Md²

Now if we put the value in a given equation it becomes,

• L (end) = (1/12) ML² + M (L/2)²
•  L (end) = (1/12) ML² + ( ¼) ML²
• L (end) = (⅓ ) ML².

Moment of Inertia of Rod Calculation

Question#1 Moment of Inertia of Rods M & L Given

Problem: A cylindrical rod is pivoted about an axis. The axis is perpendicular to its length, which passes through one of its ends. What is the moment of inertia of that rod? Where Mass, m =5 kg, Length, L = 2.5 m.

Solution: Given Input Data:

• Mass, m =5 kg
• Length, L = 2.5 m

Find out: Moment of Inertia, I =?

Calculation: We have already learned from our Moment of inertia derivation for Rod,

Moment of Inertia, I = 1/12 ML²

Now, apply parallel axis theorem, the moment of inertia of the rod about a parallel axis which passes through one end of the rod can be written as,

• I’ = I + M (L/2)²
• I’ = 1/12 ML² + M (L/2)²
• I’ = 1/12 ML² + ¼ M L²
• I’ = 4/12 ML²
• I’ = 1/3 ML²

Now, putting the value of m =5 kg & L = 2.5 m

• I’ = 1/3 x 5 x 2.5²
• I’ = 10.4 kg m²

Hence, this is the value of the moment of inertia of that rod.

Question#2 Moment of Inertia of Rods & Rotational Kinetic Energy – M, L & ω Given

Problem: A uniform cylindrical rod with mass and length is 3 kg and 1.5 m respectively, is pivoted about an axis. The axis is perpendicular to its length, which passes through one of its ends. The instantaneous angular velocity of the cylindrical rod is 70 deg./s

• What is the moment of inertia of that rod?
• What is the value of rotational kinetic energy?

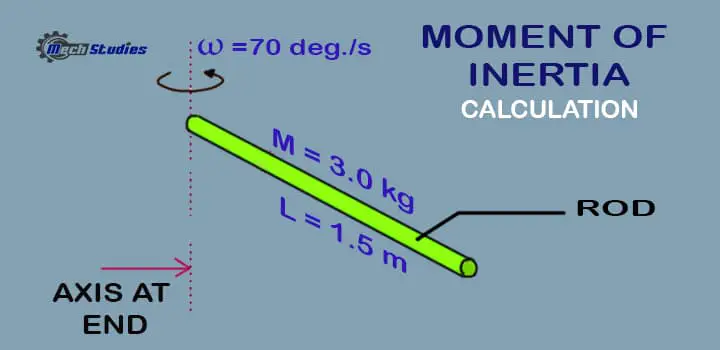
Solution: Input Data:

• Mass, m =3 kg
• Length, L = 1.5 m
• Angular velocity, ω =70 deg./s

Find out:

• Moment of Inertia, I =?
• Rotational Kinetic energy, K.E =?

Calculation: We have already learned from our Moment of inertia derivation for Rods,

Moment of Inertia, I = 1/12 ML²

Now, apply parallel axis theorem, the moment of inertia of rod about a parallel axis which passes through one end of the rod can be written as,

• I’ = I + M (L/2)²
• I’ = 1/12 ML² + M (L/2)²
• I’ = 1/12 ML² + ¼ M L²
• I’ = 4/12 ML²
• I’ = 1/3 ML²

Now, putting the value of m =3 kg & L = 1.5 m

• I’ = 1/3 x 3 x 1.5²
• I’ = 3.38 kg m²

Hence, this is the value of the moment of inertia of that rod. Now, we have got the angular velocity in deg./s, so, we have to change it first into rad/s.

• 180 deg./s = π rad/s
• 1 deg./s = π/180 rad/s
• 70 deg./s = π/180 x 70 rad/s = 1.22 rad/s
• ω = 1.22 rad/s

What is rotational kinetic energy? We know the formula,

Rotational Kinetic energy, K.E

• K.E = ½ I’ ω²
• K.E = ½ x 3.38 x 1.22²
• K.E = 2.52 Joule

Hence, the value of rotational kinetic energy is 2.52 Joule.

Question#3 Moment of Inertia of Rod when it’s Bent – M, L & Angle Given

Problem: A uniform cylindrical rod with mass and length is M kg and L m respectively is pivoted about at the center of its axis. Now, if the rod is bent at the middle to make an angle at 60 deg., what will be the moment of inertia for the same rod about the same axis?

Solution: Input Data:

• Mass = M kg
• Length = L m
• Angle between two halves = 60 deg.

Find out: Moment of Inertia, I =?

Calculation: We have already learned from our Moment of inertia derivation of Rods,

Moment of Inertia, I = 1/12 ML²

Now, apply parallel axis theorem, the moment of inertia for rods about a parallel axis which pass through one ends of the rod can be written as,

• I’ = I + M (L/2)²
• I’ = 1/12 ML² + M (L/2)²
• I’ = 1/12 ML² + ¼ M L²
• I’ = 4/12 ML²
• I’ = 1/3 ML²

Now, if the Rod is bent into two halves,

• Each part Length L’ = L/2 m

So, what will be the moment of inertia for these Rods which are bent?

• I’’ = 2 x I’
• I’’ = 2 x 1/3 M’L’³
• I’ = 2 x 1/3 M x (L/2)³
• I’ = 2 x 1/3 M x L³/8
• I’ = 1/12 ML³

Hence, the moment of inertia of that rod will become 1/12 ML³ kg m²

Conclusion

Hence, we have learned the basics of the moment of inertia of rods and also learned how to calculate this value along with sample calculation.