What is Hooke’s Law in Stress-Strain? Definition, Equation, Formula, Graph, Example

What is Hooke’s Law in Stress-strain? Any idea! In this article, we will learn the basics of this law, along with the definition, equation or formula, graph, example, etc. Let’s explore!

What is Hooke’s Law in Stress-Strain? Basics

Let’s try to understand the basics of Hooke’s law! Looking around us we constantly ask ourselves questions such as is this rubber band elastic?

• Is this pair of jeans stretchable elastic?
• What makes a rubber elastic and what makes wood inelastic?
• Can the property of elasticity be lost or regained?
• Is steel elastic?

To know all these things, we need to dive into the concept of elasticity and plasticity, most importantly Hooke’s law.

• We all have wooden scales or steel scales. Generally, when we play we try to bend them. When we try to bend the wooden scale, it bends a little bit for a second but in the next second, it snaps and gets broken. Now it will stay like that forever. Well in layman terms it is plasticity.
• But in other cases when we try to bend the steel scale it bends quite easily and when we remove force on its ends, it regains its original shape then that is elasticity.

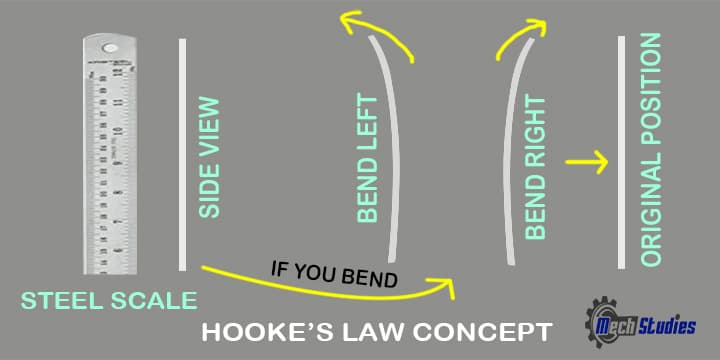
No matter how many times you do it, it will regain its shape. But if add too much force and try to bend it exactly 180 degrees in the middle then that same steel scale will break and that is plastic behavior shown by it.

Hooke’s Law Basic Terms

Before understanding Hooke’s law, we need to understand some basic properties.

Elasticity

• It is ability of material to regain its shape and size after the removal of external applied force to its original shape and size after the deformation.
• All metals are generally elastic, but its value varies as per specific material composition.

Example: Steel cables

Plasticity

• It is the ability of the material to permanently to take the deformed shape after application of external load, i.e., stay deformed permanently.

Example: Plastic

Stiffness or Rigidity

• It is the ability of a material to give the resistance to the deformation under the action external applied force.
• All metals deform under load, but it is their resistance which is offered that is important and it is measured by the young’s modulus. Within the elastic limit if that material deforms less, such material is considered of having high stiffness.

Resilience

• It is the ability of material to absorb the energy when it is deformed elastically and release the same when that load is removed.
• It is generally measured by the modulus of resilience 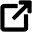and its very important while designing springs.

Toughness

• It is the ability of a material to absorb as much as energy possible before it gets ruptured/fractured.
• It is basically ability to provide resistance to impact loads. Tough material generally goes through the bends, twist, stretching before reaching till the breaking point. It is measured by modulus of toughness.

Let us quickly go through the differences between elasticity and plasticity.

Elasticity	Plasticity
If a spring/material returns to its original size and shape once you remove the forces stretching or deforming it (reversible deformation), we are saying that the fabric is demonstrating elastic behavior.	Plastic material is the one that stays deformed even after you have taken the force away. This change which is irreversible is called plastic behavior.
The amount of elastic deformation is less	The amount of plastic deformation is more.
In atomic angle, when atoms get displaced from their original position but return back when the load is removed.	When atoms get permanently displaced from their original positions and take up the new one.
For most material stress-strain relationship is linear	The stress-strain relationship is non-linear.
Elasticity is an important consideration for machine tool components.	Plasticity is an important consideration for press working operation.

• In elementary mechanics the elasticity of a spring is expressed by Hooke’s law which talks about the amount a spring is stretched or compressed beyond its relaxed length is directly proportional to the force acting on it.
• In continuous elastic materials Hooke’s law implies that strain may be a linear function of stress. Some materials that we usually consider as highly elastic, for instance rubber, do not obey Hooke’s law except under very small deformations.
• When stress gets bigger beyond limit then deformation can be seen in materials and in the end, they reach the elasticity limit after which they become plastic and stay deformed.

Hooke’s Law Spring Experiment & Example

Let’s see the Hooke’s law experiment for stress-strain as well as the theory behind this law,

Hooke’s Law Spring Experiment

Set up – There is one stand that has a hook on two sides.

• On one hook the measuring scale is kept and another side there is a spring.
• The spring has hook at its bottom so that various weights can be attached to it.
• The weights attached will act as force (W= mg).
• That way we can measure the length of spring during both position, that is when weight is applied and when weight is removed.
• The displacement (x) of a spring can be measured from measuring scale.
• This is just a crude experiment.

Let us get a basic understanding of what is Hooke’s law. As we there is one spring and at one end, the weights are attached to it. On another side, the scale tells us the elongation the spring went through.

• As we can see earlier the load is added from 1 newton to 3 newton there is linear relationship between both properties, and it goes on till 4 newtons.
• From here on there seems a little mismatch between load added the elongation in the spring.

So, till 4N there seems to be a proportional relation between the load applied and elongation but after 5N the proportional relationship breaks. And we see more weights are being added the elongation is not in a linear relationship.

So, it seems that spring reached its elastic limit somewhere near 5N, beyond which it will continue to elongate till some point after which it might break.

Hooke’ Law of Elasticity Theory

• The shape of a body will always distort when a force is applied to it. If the particular body is elastic in nature. It may get distort by compression or tension and it may go back return to their original position when the distorting force or the applied force is removed (it goes without saying that all this applies with an elastic limit of material).
• Hooke’s Law states that if the distortion of an elastic body is not over large region, the force tending to revive the body to equilibrium is proportional to the displacement where F may be a restoring force, k may be a constant of proportionality and x is that the distance the thing has been displaced from its equilibrium position.
• The minus (-ve) sign signifies that the restoring force acts in an opposite direction to the displacement of the body from the equilibrium position.

Here spring obeys Hooke’s Law, it is displaced from equilibrium and follows “simple harmonic motion”. Because it oscillates due to the weight added to it.

Many processes show this SHM. Some common examples are water waves, sound waves.

𝐹 = −𝑘𝑥

For springs this relation is termed as Hooke’s Law.

• The burden of a mass suspended to the tip of a spring is that the stretching force acting on the spring.
• We are hanging completely different weights to the tip of a spring due to this activity of the extensions which enables spring to respond to squeezing and elongating force.
• The value of k gives information of stiffness. A stiff spring can have greater value for k; a softer spring can have a smaller value of k. The spring constant is measured in newtons per metre.
• Once the mass is persisted the spring then displaced from its equilibrium position, it’s going to oscillate up and down.
• The restoring force equipped by the spring is sometimes directed back towards the equilibrium position.

Hooke’s Law Spring Constant

The constant of proportion ‘k’ is called the spring constant and will be found by subjecting the spring to force and by calculating displacement. So, from values of F and x we can find the stiffness of the spring we just tested through this experiment.

The unit of Hooke’s law spring constant is N/m (S.I unit)

Hooke’s Law Statement, Equation or Formula, Graph

Hooke’s Law Statement

Hooke’s Law statement is written as,

The amount a spring goes through extension is directly proportional to the amount of force applied to it.

The spring constant is used to measure how stiff the spring actually is. The stronger the spring, the greater is the spring constant.

Hooke’s Law Equation or Formula

From the experiment as well as the statement, we have got that,

F = – k.x

Where:

• F is that the applied force (in newton, N),
• x is that the extension (in metres, m) and
• k is that the spring constant (in N/m).
• The extension x is typically written or∆x.
• x = changed in length (i.e., stretched length – original length)

Notes

1. The negative sign indicates that the direction of the spring force is often to the opposite to displacement of the spring.
2. The spring constant measures however stiff the spring is. If the spring constant value is larger, the spring stiffness is also larger. That means it will be very hard to stretch or extend it.

Hooke’s Law Graph

Let’s see the simple graph of Hooke’s law,

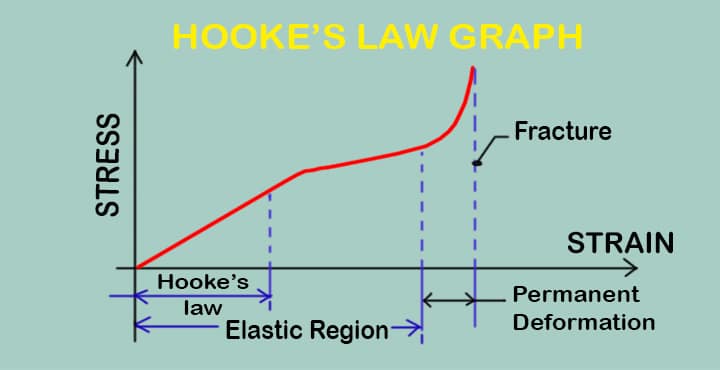
Stiffness of spring

If we plot the graph of force on the x-axis and extension on the y-axis, then the stiffness of a spring can be plotted with both values.

• If the slope of the graph will be more then that spring is stiff spring.
• If the slope of the graph will be 45 degrees, then that spring is soft spring.
• If the slope of the graph will be smaller than 45 degrees, then spring is even softer.

This is the general practice of reading Hooke’s law graph; the stiffness k is measured in unit newton per meter. You can check the stress-strain diagram for details.

Practical Example of Hooke’s Law in Automobile Seatbelt

Elastic behavior is extraordinarily necessary for automobile safety, as automobile seatbelts are created from elastic materials. However, when a car crash has happened it becomes necessary to get them replaced.

Why?

• Because during an accident they acted as a restoring force to control the body which was thrown forward by the inertia. So, there is good possibility that they withstand that force which was beyond their elastic limit.
• So, if such accident happens again, they might exhibit their full potential because now they might not be totally elastic. Why seat belts have to be very elastic? Why can’t we have rigid seatbelts which may keep you firmly in place?
• If a rigid belt is used that it will slow your body too quickly it might hurt you and elastic belt brings comfort by decreasing the speed slowly without a sudden jerk.
• Elasticity will be dependent on collision force, and it will act in its proportion, this ability cannot be achieved by rigid belt.

Young’s Modulus & Hooke’s Law Spring Constant

• Almost any solid body, anchored at one side and forced at the alternative side, can react in a style of a spring. Basically, this reflects those interatomic forces are generally close to elastic, once the atoms get solely displaced slightly off from their positions, they try to achieve earlier position when force is removed.
• Several elastic bodies that we use daily are an example rubber bands, wire, water hoses. These all are long rod-like objects with constant cross section, usually created of solid and isotropic material without any specific internal structure. Their uniform composition and easy kind of construction create such rods convenient models for real, material springs.
• The force F = kx is necessary to increase the length L of a rod-like material spring by a small quantity x should be proportional to the area, A, of the spring’s cross section.
• Stress is given by force/area then that gives us σ = F/A = kx/A. as F is acting over all spring, then stress will be same all over the place.
• Likewise, for a smaller piece of the spring of length L'< L, the uniformity implies that it will be stretched proportionately less such x’/l’ = x/L. This mean for a spring that extension value is too small, and x will not direct change in length of spring but a relative change in it.
• Strain is given by ε = x/L. by putting all this value in formula young’s modulus= stress/strain

Young modulus, E

• E = σ / ε
• E = (F/A) / (x/L)
• E = (k . x /A) / (x/L) [as F = kx]
• E = (k . L /A)
• k = E. A/L

Poisson’s Ratio vs Hooke’s Law Spring Constant

Normal materials generally contract in the direction which is perpendicular to the direction in which it is going through extension. If the cross-section of “diameter” d of a rod-like spring changes by Δd, the lateral strain becomes of the order of εd = Δd/d, and it will be negative for an extension caused by force F.

In linearly elastic materials, Δl is the increase in length with respect to the original length, l

The negative value of this quantitative relation

• ν = (-) ε_d / ε_l
• ν = – (Δd/d)/(Δl/l)

This ‘ν’ is called Poisson’s ratio. Poisson’s ratio is dimensionless. It generally lies between -1 and +0.5, though it’s continuously positive for natural materials. Typical values for metals laze zero 0.30.

Limitations of Hooke’s Law

There are a few limitations of Hooke’s law, as follows:

• Hooke’s law for isotropic materials, expressed by the linear relationship between stress and strain, is just valid for stresses up to a specific limit known as the proportionality limit. Beyond this limit, nonlinearities come into the picture, and so this formalism becomes invalid.
• Eventually a point is achieved, known as the elastic limit, wherever the material stops behaving like an elastic and undergoes permanent deformation and turns plastic. Within the finish Line the fabric/material might even fracture.
• Hooke’s law is, however, an awfully sensible approximation for many metals beneath traditional conditions wherever stresses are small compared to the elastic moduli.
• While repeated application also affects material and causes fatigue. It is not just the elastic limit but the repetition cycle, material properties and fatigue also affect material elasticity.

Hooke’s Law Calculation Example

Calculation: A spring is hooked from a fixed stick. It is displaced by 10 cm by a force of 550 N applied to it. Find out the spring constant.

Solution: Let’s see what are the data are given in the question!

• F = applied force = 550 N
• x = displacement = 10 cm
• x = 0.1 m [ Since, force F is in S.I unit, displacement is changed into S.I unit]

Now, from the formula of Hooke’s Law, we can write,

• F = – k.x
• 550 = – k x 0.1
• k x 0.1 = – 550
• k = 5500 N/m

Hence, the spring constant of the spring is 5500 N/m.

Applications of Spring

Springs are mechanical elements that absorb energy, exert force or torque as per respective needs.

• Toys
• Suspension system – Railway, vehicles.
• Landing gears of aeroplanes
• Clocks and measuring instruments.

Conclusion

Hence, we have got the basic idea of Hooke’s law along with definition, equation, or formula or graph, etc. Any doubt, please write to us!