Bernoulli’s Principle: Equation, Derivation, Applications

Bernoulli’s principle as well as equation is explained along with basic details, statement, derivation, applications, etc. in this article. This is the very basic principle based on we which we all are standing, developing, and making progress towards innovation. Let’s explore Bernoulli’s equation!

Bernoulli’s Principle & Equation

Let’s get in Bernoulli’s principle! Numerous things can be explained through some of the principles. Delving about different concepts such as the working of an airplane needs the understanding of Bernoulli’s theorem. If you are also keen to understand the answer to some of the different phenomena related to fluid mechanics, this excerpt will be of utmost value.

Let’s delve into the all-round information about one of the basic principles. Have you ever wondered how a boat keeps on moving in the stream?

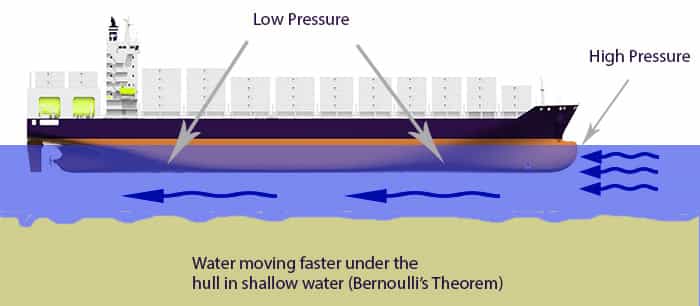
• The primary and simplistic approach towards the reason is that the water flows around the boat thew generates higher pressure under the boat body.
• However, understanding the core concept behind this needs an understanding of fluid mechanics, specifically, the principle called the Bernoulli equation.
• This equation doesn’t only help you to get an understanding of the boat’s movement but also provides holistic information about the Airplane’s movement.
• This principle can even understand the effect of force on a skyscraper of the high winds or water speed out of your water hose.

What is the Bernoulli’s Equation?

Basic of Bernoulli’s Equation

The Bernoulli equation states explicitly that an ideal fluid with constant density, steady flow, and zero viscosity has a static sum of its kinetic, potential, and thermal energy, which cannot be changed by its flow. This generates a relationship between the pressure of the fluid, its velocity, and the relative height.

Bernoulli’s Statement

Specifically, the Bernoulli equation states that:

”In fluid dynamics, Bernoulli’s principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid’s potential energy”

It implies that the summation of pressure energy, kinetic energy & potential energy is always constant at any point of a streamline for an incompressible fluid.

Bernoulli’s Equation

As per Bernoulli’s principle,

Pressure energy (P.E) + Kinetic Energy (K.E) + Potential Energy (Pt.E) = Constant.

That means,

P.E + LK.E + Pt.E = Constant.

P₁ + 1/2ρv₁² + pgh₁ = P₂ + ½ ρv₂² + pgh₂ = Constant

where v is the fluid velocity,

• ρ is the fluid density,
• h is relative height,
• P is pressure

It is easy to understand this equation with the help of this example. Let’s take a reservoir that is situated at the top of the mountains. The attachment of pipe for water flow to the town is connected at a lower height.

• The Bernoulli equation helps us deduce the water’s speed that will flow into the plant turbines of a hydroelectric plant.

• This is the core example that helps us to understand the application of this principle effectively.

Apart from this, there is a different phenomenon that can be understood with the help of this principle. This principle is applied to numerous things such as atomizer, carburetor, venturi meter, and aspirator.

Meaning of Bernoulli’s Equation

This equation is explicitly the statement of the conservation of energy for a flowing fluid. Specifically, the equation shows the qualitative behavior through which pressure gets low in the regions where the velocity is high. This is credibly known as the Bernoulli effect.

Importance of the Bernoulli’s equation

Daniel Bernoulli deduces the Bernoulli equation in which the speed of fluid affects the fluid pressure. It is also known as Bernoulli’s effect.

• It also describes the kinetic theory of gases.
• Daniel Bernoulli has provided both of these deductions, and these made him famous.
• According to this theory, when a fluid flows through a path in which its speed increases, it decreases in pressure.
• There are numerous applications of this principle in our daily life.

History of the Bernoulli’s Principle

Being one of the main principles in fluid mechanics, Bernoulli’s principle helps us to explicitly understand that the decrease in static pressure or potential energy co-occurs with the increase in a fluid’s speed.

• Daniel Bernoulli had given this principle. He published this principle in his book called “Hydrodynamical” in the year 1738. Daniel Bernoulli has deduced that with the flow speed increase, there is a decrease in pressure, but there was a slight change, concluded by Leonhard Euler, who has provided us with this usual form of Bernoulli equation in the year 1752.
• However, this principle is only applied to isentropic flows. Here the effects of non-adiabatic processes and irreversible processes are mere or can be neglected. The typical example of both is heat radiation and turbulence, respectively.

Derivation of Bernoulli’s Equation

Suppose a pipe that has varying height and diameter. An incompressible fluid is flowing through this pipe.

Bernoulli’s Principle Assumption

There are a few assumptions of this principle,

• The first assumption is that the fluid is flowing through a pipe or flowing through a channel.
• Flow is steady (no change of velocity at any point).
• Incompressible fluid (no change of density) the density remains constant at any points.
• Negligible frictional force.
• There will not be any rotational speed in the fluid.
• No heat transfer in the flow.
• There are no viscous forces in the fluid, the energy is conserved

Bernoulli’s Equation Derivation

Consider a pipe with varying diameter and height through which an incompressible fluid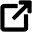 is flowing.

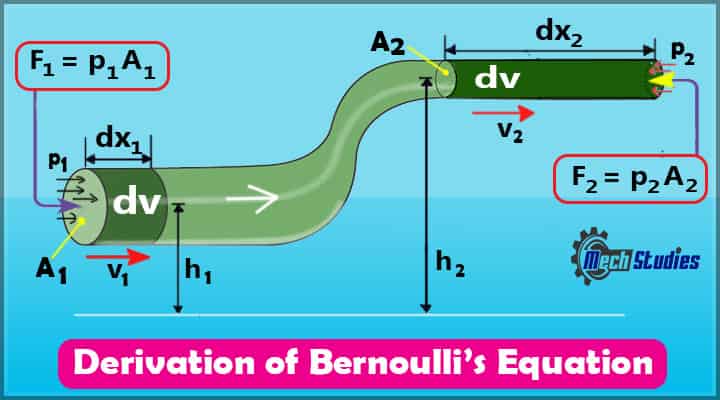
The relationship between different attributes of the pipe as well as fluid are:

• A – the areas of cross-sections,
• v – the flow speed,
• y – height from the ground,
• p – pressure at two different points

Now, we can deduce the work done of the fluid as follows:

• DW = F₁dx₁ – F₂dx₂
• DW = p₁A₁dx₁ – p₂A₂dx₂ [as F = pA ]
• DW = p₁dV – p₂dV = (p₁ – p₂)dV

We know that the fluid’s work is due to the change in kinetic energy and conservation of gravitational force.

The change in kinetic energy can be deduced as

dK=1/2m₂v₂²−1/2m₁v₁²=1/2ρdV(v₂²−v₁²) [ as m₁ =m₂ = ρdV]

Change in potential energy is given as:

dU = mgh₂ – mgh₁ = ρdVg(h₂ – h₁) [ considering m₁ =m₂ = m]

The overall energy equation is given as:

• dW = dK + dU
• (p₁ – p₂) dV = 12ρdV (v₂²−v₁¹) + ρdVg (h₂ – h₁)
• (p₁ – p₂) = 12ρ (v₂²−v₁²) + ρg (h₂ – h₁)

Arranging the equation in its simplest form, we get

p₁+1/2ρv₁²+ρgh₁=p₂+1/2ρv₂²+ρgh₂

This is the known as Bernoulli’s equation.

Bernoulli’s Principle for Fluid Conditions

There are two basic conditions of fluids,

Bernoulli’s Principle for Static Fluids

Fluid is static means velocity is zero.

That means, v₁ = v₂ = 0

From Bernoulli’s equation, p₁+1/2ρv₁²+ρgh₁=p₂+1/2ρv₂²+ρgh₂

Hence, p₁+1/2ρ. 0²+ρgh₁=p₂+1/2ρ. 0²+ρgh₂

or, p₁ + ρgh₁=p₂ + ρgh₂

Bernoulli’s Principle for Constant Depth

Constant depth means no change in depth.

That means, h₁ = h₂

From Bernoulli’s equation, p₁+1/2ρv₁²+ρgh₁=p₂+1/2ρv₂²+ρgh₂

Hence, p₁+1/2ρv₁²+ρgh₁=p₂+1/2ρv₂²+ρgh₂

or, p₁+1/2ρv₁²+ρgh₁=p₂+1/2ρv₂²+ρgh₁ [as h₁ = h₂]

or, p₁+1/2ρv₁² =p₂+1/2ρv₂²

Applications of Bernoulli Principle

Bernoulli equation is the core of different processes. It has wide applications that make help us to find out the followings,

• Pressure energy
• Pressure head
• Kinetic energy
• Velocity of fluid
• Elevation level
• Flow rate
• Velocity potential
• type of flow etc.

Here we are providing some of the core applications that makes it quite efficient:

Pump & Pipe Sizing

• We have already seen kinetic energy conversion into pressure energy in centrifugal pumps. This is a very simple example of Bernoulli’s equation.
• The velocity of water through the pipe as well as in case of pipe design Bernoulli’s equation is referred.

Parallel movement of boats

• It is seen that whenever two boats are moving in parallel motion in the same direction, the air and water movement gets gradually fast as compared to the boats carrying opposite sides.
• Bernoulli’s principle states that the force between the two boats gets decreases, which pulls the boat to each other due to the change in pressure.

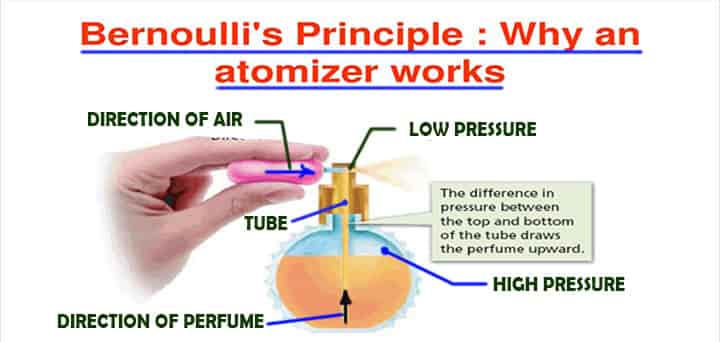
Atomizer

• The atomizer is a core part mainly used in insect sprayers, carburetor, paint gun, and different other things that have similar functions. 
• The high airspeed is in play, which passes through the tube that is immersed in the fluid to spray.
• This is because of the motion of the piston in the cylinder. Here comes the Bernoulli theorem’s application, which entails that the rise in the fluid creates less pressure, resulting in providing the fluid high speed.

Working of a chimney

• One of the typical applications of Bernoulli theorems is in the chimney of our home.
• The smoke is blown away to the low-pressure area as the wind velocity above the chimney’s nozzle increases, which helps the air rush outside.
• The application of the Bernoulli principle is quite useful. Thus, we get an understanding of why chimneys work far better in the high wind flow.

The flying motion of Airplane

Have you ever imagined how does the airplane fly? If you are unaware of this fact, then get in mind that this also happens due to Bernoulli’s theorem.

• As we all know, the plane’s wings have a particular shape, and when the plane moves, air flows above its high speed compared to the low surface wing.
• There is a difference in the airflow above and below the wings due to Bernoulli’s principle.
• Due to this, the change in pressure occurs, which results from the flow of air on the up surface of the plane’s wing.
• The plane rises when the force gets higher than that mass of the plane.

Blowing of Roofs

• This is a natural fatality in which the roofs of the huts blow off.
• The blowing wind generates low weight on the roof, which also increases the force under the roof compared to low pressure.
• The difference in pressure causes the roof to be raised; hence it gets blown off.

Siphon

Siphon is widely used to empty a tank or transfer from one tank to another if these are separated by a barrier.

Magnus effect

Have you imagined why football attains a different path if a player takes a shot?

• This is due to Bernoulli’s theorem.
• It happens when a rotating ball.
• Sometimes it deviates from its ordinary course.
• This is effectively known as the Magnus effect.
• It happens in different sports such as soccer, tennis, and many other games as well.

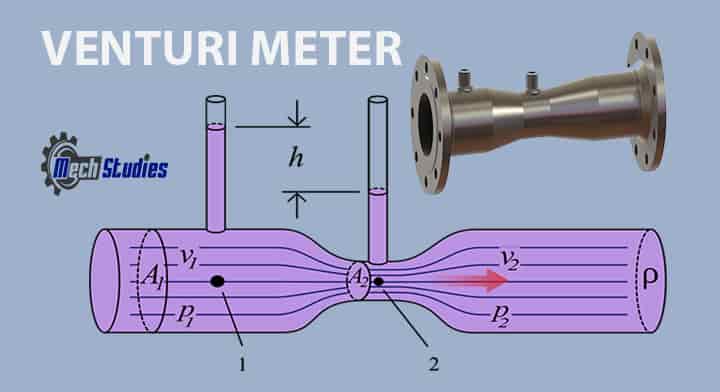
Venturi Meters or Orifice Plate

• Venturi meter or orifice plate is another best example of Bernoulli’s principle. These are widely used for the measurement of fluid flow.

Pitot Tube

The pitot tube is used to measure the pressure in various industries and it works based on Bernoulli’s principle.

Real-life applications of Bernoulli’s principle

This is one of the common questions that come into the mind while understanding this concept. The use of the Bernoulli principle is vivid. The foremost use of this principle is in the flying movement of airplanes. People often wonder how an airplane attain its flying motion. If you are aware of this principle, then you will be able to understand the fact behind the former easily.

Bernoulli’s Principle Calculation Example

The absolute pressure of water in a pipe is 1.02 x ₁₀⁵ N/m² when the water is flowing at 1.7 m/s. Find out the absolute pressure if the velocity of water is changed into 23 m/s. Consider that there is no friction in the fluid flow and density of water is 10³ kg/m³

Let’s try to solve it.

Input data given

• Pressure at condition 1, p₁ = 1.02 × 10⁵ N/m² 
• Velocity of water at condition 1, v₁ = 23 m/s
• Velocity of water at condition 2, v₂ = 1.7 m/s
• Density of water, ρ = 10³ kg/m³

Data to Find out

Absolute pressure, p₂ =?

From Bernoulli’s equation,  

p₁+1/2ρv₁²+ρgh₁=p₂+1/2ρv₂²+ρgh₂

=> p₁+1/2ρv₁² =p₂+1/2ρv₂²

=> p₂+1/2ρv₂² = p₁+1/2ρv₁²

=> p₂ = p₁+1/2ρv₁² -1/2ρv₂²

=> p₂ = 1.02 × 10⁵ +1/2 × 10³ × 23² – 1/2 × 10³ × 1.7²

=> p₂ = 3.65 × 10⁵ N/m²

Limitations of Bernoulli’s Principle

There are some aspects where there is ambiguity in the application of the Bernoulli theorem. The following are the set of limitations regarding the Bernoulli theorem:

• While deducing the equation, the fluid must be incompressible.
• The viscous effect should be minimal.
• In this theorem, the external force of any kind will effectively cause the change in fluid flow.
• This theorem is applied to non-viscous fluid only.
• If the fluid flow is curved, then the energy generated due to centrifugal forces should be considered.
• The fluid flow should not change concerning time.
• Often in a viscous flow, partial energy gets lost due to the sheer force, while in unstable flow, a sheer amount of kinetic energy gets converted to heat energy. While deducing the equation, these losses should be considered.
• This equation is not suitable for non-steady and turbulent fluid flow. It applies to a supply of liquid that is streamlined.
• Friction in the tube plays a vital role as the velocity of the fluid particle in the midsection is maximum and gradually gets decreased in the direction of the tube. Here the liquid velocity doesn’t get considered while mean velocity is in use as the former is not consistent throughout.

Summary

The Bernoulli equation is a vital expression that correlates the height, velocity, and pressure of a fluid concerning its flow. This relationship helps us to understand the condition of the fluid, which remains streamline.

• This takes place in an idealized system, which refers to a fluid with inviscid and incompressible properties.
• The holistic changes in these properties can be deduced with this principle.
• In this excerpt, we have provided some of the core information and derivations, which helps to understand the fluid flow’s core concept.
• This equation and its applications are vivid, from pipe flow to wing design, from venturi meter to Bunsen burner.

The application of Bernoulli’s equation is quite efficient. However, there is a massive description of this equation that can be further considered. If you want to understand one of the core concepts related to fluid mechanics, then the above information is ample.

Refer our YouTube Videos